Performance evaluation of Double Recycled Reclaimed Asphalt Pavement (DRRAP) at low temperature

Ki-Hoon Moon

doi:10.22702/jkai.2020.10.2.017

Preview

Scientific Paper

Journal of the Korean Asphalt Institute. 31 December 2020. 196-203
https://doi.org/10.22702/jkai.2020.10.2.017

Performance evaluation of Double Recycled Reclaimed Asphalt Pavement (DRRAP) at low temperature

Ki-Hoon Moon¹^*

¹Senior Researcher (Ph.D.), Korea Expressway Corporation Pavement Research Division (KECPRD)

^{*Corresponding Author}

ABSTRACT

To mitigate environmental issue and budget reduction problem application of recycled asphalt material so called Reclaimed Asphalt Pavement (RAP) is essential in asphalt pavement industry. For many decades, many pavement agencies successfully applied RAP on the actual asphalt pavement construction. Moreover, interest and application of Double Recycled Reclaimed Asphalt Pavement (DRRAP) got more attractions for pavement engineer for many years. However, it needs to be known that stiffer and more brittle characteristics of RAP compared to the conventional asphalt pavement material provide negative effect on pavement performance especially at low temperature condition. In this paper, performance evaluation of DRRAP compared to the conventional Single Recycled Reclaimed Asphalt Pavement (SRRAP) materials at low temperature was performed by means of simple mathematical approach. As a result, possibility of DRRAP application on actual pavement work was derived.

Keywords

Low temperature cracking

Double Recycled Reclaimed Asphalt Pavement (DRRAP)

Single Recycled Reclaimed Asphalt Pavement (SRRAP)

Thermal Stress (TS)

MAIN

1. Introduction
2. Material preparations and experimental works
3. Performance evaluation parameter
4. Data analysis
5. Summary and conclusion

1. Introduction

Moreover, interest and application of Double Recycled Reclaimed Asphalt Pavement (DRRAP) got more attractions for pavement engineer for many years in Japan and United Kingdom (Heneash, 2013; Kareem et al., 2019). Fortunately, possibilities of DRRAP application on actual pavement construction was derived by means of testing construction and follow-up surveying effort. However, it needs to be known that stiffer and more brittle characteristics of RAP compared to the conventional asphalt pavement material provide negative effect on pavement performance especially at low temperature condition.

It is well known that low temperature cracking is one of serious pavement distresses on asphalt pavement (Moon et al., 2013; Moon et al., 2014; Mon et al., 2017). Water infiltration on pavement layer can easily be happened due to low temperature cracking and this can finally lead macro cracking, deformations and several pot holes. Due to this reason many pavement agencies tried to develop reasonable testing method to evaluate low temperature performance of given asphalt material and finally low temperature creep test was developed (Moon et al., 2013; Moon et al., 2014; Moon et al., 2017). Creep stiffness, creep compliance and thermal stress can be successfully the evaluating parameter for low temperature performance of given asphalt material.

In this paper, performance evaluation of DRRAP compared to the conventional Single Recycled Reclaimed Asphalt Pavement (SRRAP) materials at low temperature was performed by means of simple mathematical approach.

2. Material preparations and experimental works

A total of four different asphalt mixture materials with PG 64-22 of asphalt binder were prepared in Korea Expressway Corporation Pavement Research Division (KECPRD). The following steps represent the production of SRRAP and DRRAP materials in this paper.

First, the virgin asphalt mixture was generated based on current specification (MOLIT, 2017) then stored on the oven at 125ºC for 65 hours to artificially generate aged asphalt mixture. Secondly, the aged mixture was mixed with the virgin asphalt mixture to generate SRRAP mixture. Then these SRRAP mixtures were stored in the oven at 125ºC for 65 hours to artificially generate aged asphalt mixture again. Finally, the aged SRRAP mixture was mixture with virgin asphalt mixture to generate DRRAP mixture. A summary information of prepared asphalt materials in this paper is presented in Table 1. It needs to be mentioned that RAP mixing proportion was set as 25%; generally used for actual RAP mixing proportion rate on asphalt mixture production in South Korea. Fig. 1 shows the prepared asphalt mixture samples in this paper.

Table 1.

prepared asphalt mixtures in this paper

Mix ID	Recycling Level	Asphalt Binder (PG)	RAP (%)	NMAS (mm)	Aggregate gradation (Aggregate size: mm / Passing: %)	Target Air Voids (%)
1	SRRAP	64-22	25	12.5	(13/93),(10/77),(5/53),(2.5/33),(0.6/21), (0.3/14),(0.15/12),(0.08/6)	4.2~4.9
2	DRRAP	64-22	25	12.5	(13/92),(10/78),(5/52),(2.5/34),(0.6/22), (0.3/15),(0.15/12),(0.08/6)	4.2~4.9

NMAS : Nominal Maximum Aggregate Size

SRRAP: Single Recycled Reclaimed Asphalt Pavement

DRRAP: Double Recycled Reclaimed Asphalt Pavement

https://static.apub.kr/journalsite/sites/jkai/2020-010-02/N0850100204/images/jkai_10_02_04_F1.jpg

Fig. 1

prepared asphalt mixtures (SRRAP and DRRAP)

To evaluate low temperature performance of SRRAP and DRRAP mixtures, Bending Beam Rheometer (BBR) mixture creep test was prepared then performed (Marasteanu et al., 2009). Rather than applying 980mN of constant load for 240 seconds, approximately 4,000~6,000mN was constantly applied for 1,000 seconds in BBR mixture creep test. Information of BBR mixture creep test is presented in Table 2 and Fig. 2, respectively.

https://static.apub.kr/journalsite/sites/jkai/2020-010-02/N0850100204/images/jkai_10_02_04_F2.jpg

Fig. 2

Bending Beam Rheometer (BBR) mixture creep test

Table 2.

Information of BBR mixture testing

Mix ID	Binder Type	Test temperature [Number of replicates]	Applied load [Testing temperature]
1,2	PG 64-22	lowPG+10°C: -12°C [5] low(PG+10)-12°C:-24°C [5]	4,000 ± 40 mN [-12°C] 6,000 ± 60 mN [-24°C]

3. Performance evaluation parameter

In this paper, Thermal Stress (TS) was considered as major parameter for performance evaluation of given mixture at low temperature condition. Thermal Stress (TS) can be computed based on the following computation process. In BBR mixture test (Marasteanu et al., 2009), creep stiffness: S(t), and m-value: m(t), can be computed as:

(1)

\{\begin{cases} S (t) = \frac{1}{D (t)} = \frac{σ}{ε (t)} = \frac{P \cdot l^{3}}{4 \cdot b \cdot h^{3} \cdot δ (t)} \\ m (t) = |\frac{d L o g S (t)}{d L o g (t)}| ≅ |\frac{d (A_{1} \cdot [L o g (t)]^{2} + A_{2} \cdot L o g (t) + A_{3})}{d L o g (t)}| \end{cases}

Where, S(t) : time-dependent flexural creep stiffness (=MPa);

D(t) : creep compliance (=1/MPa);

$σ$ : bending stress in the beam (=MPa);

$ε$ (t) : time-dependent bending strain in the beam (=mm/mm);

P : applied constant load (=mN);

$δ$ (t) : beam deflection (=mm);

l, b, h : beam dimensions (l=102, b=12.7, h=6.25, mm);

t : time (=sec);

A₁, A₂, A₃ : fitting constants

Based on the linear viscoelastic theory, relaxation modulus: E(t), can be computed as:

(2)

\{\begin{cases} \int_{0}^{t} E (t - τ) \cdot D (t) d τ = t \\ \int_{0}^{t} E (t) \cdot D (t - τ) d τ = t \end{cases}

In Equation (2), relaxation modulus: E(t), and corresponding creep compliance: D(t), can be approximated based on several previous experimental works as:

(3)

D (t) = D_{1} \cdot t^{n}, E (t) = E_{1} \cdot t^{- n}

Equation (3) can be re-expressed based on Laplace transformation as:

(4)

L (\int_{0}^{t} E (t - τ) \cdot D (t) d τ) = \frac{1}{s^{2}}

Through Gamma function analysis and Euler reflective formula, E(t) can be expressed as:

(5)

E (t) \cdot D (t) = \frac{s i n (n \cdot π)}{n \cdot π} \Rightarrow E (t) = \frac{1}{D (t)} \cdot \frac{s i n (n \cdot π)}{n \cdot π}

(6)

n = {|\frac{d l o g D (t)}{l o g τ}|}_{τ = t} o r n = {|\frac{d l o g E (t)}{l o g τ}|}_{t a u = t}

Then construct relaxation modulus: E(t), master curve through Christensen-Anderson-Marasteanu (CAM) model as (Marasteanu et al., 2009):

(7)

E (t) = E_{g} \cdot [1 + {(\frac{t}{t_{c}})}^{v}]^{- \frac{w}{v}}

Where, E_g = glassy modulus, assumed equal to 30~40GPa for asphalt mixtures,

t_c, v and w = fitting parameters.

a_T = shift factor can be expressed as:

(8)

a_{T} = 10^{C_{1} + C_{2} \cdot T_{s}} \Rightarrow L o g a_{T} = C_{1} + C_{2} \cdot T_{s}

By using Equations (1) to (8) and solving Equation (9) numerically, TS of given asphalt mixture can be computed as:

(9)

σ (t) = \int_{- \infty}^{t} \dot{ε} (t) \cdot E (t - t') d t' \Rightarrow σ (ξ) = \int_{- \infty}^{ξ} \frac{d ε (ξ')}{d ξ'} \cdot E (ξ - ξ') d ξ' = \int_{- \infty}^{t} \frac{d (α \cdot ∆ T)}{d t'} \cdot E (ξ (t) - ξ' (t)) d t' \Rightarrow σ (ξ) = \int_{- \infty}^{ξ} \frac{d ε (ξ')}{d ξ'} \cdot E_{g} \cdot {[1 + {(\frac{ξ - ξ'}{t_{c}})}^{v}]}^{- \frac{w}{v}} d ξ' = \int_{- \infty}^{t} \frac{d (α \cdot ∆ T)}{d t'} \cdot E_{g} \cdot {[1 + {(\frac{ξ (t) - ξ' (t)}{t_{c}})}^{v}]}^{- \frac{w}{v}} d t'

(10)

ξ = \frac{t}{a_{T}} \Rightarrow L o g ξ = L o g t - L o g a_{T}

(11)

ε (t) = α \cdot ∆ T

$α$ = Coefficient of thermal expansion or contraction assumed as: $α$ = 0.00003 (Moon et al., 2013),

$∆ T$ = temperature cooling rate (-2ºC/hour of cooling rate was considered)

4. Data analysis

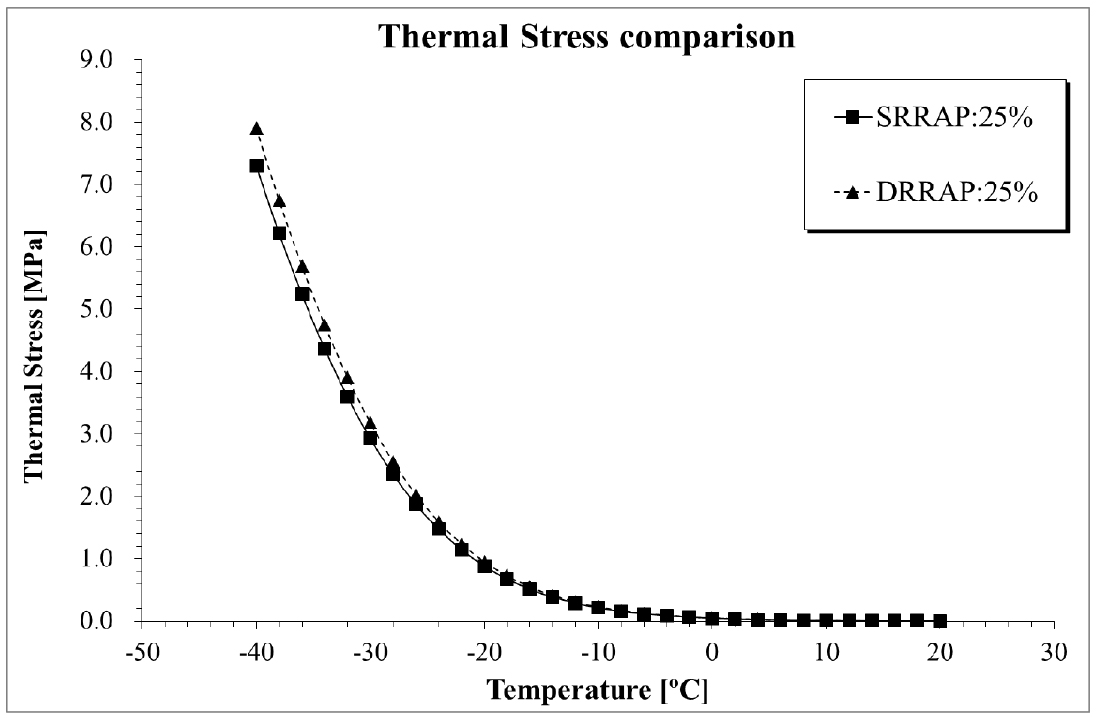
Based on Equations (1) to (11), thermal stress was computed then compared. The result is presented in Fig. 3 and Table 3.

From the results in Fig. 3 and Table 3, it can be observed that not significant differences on thermal stress computation results were observed between SRRAP and DRRAP mixtures. At the lowest temperature condition (i.e -40ºC), the difference rate was 7.7% (=0.6074/7.9021) which supports the findings in this paper.

https://static.apub.kr/journalsite/sites/jkai/2020-010-02/N0850100204/images/jkai_10_02_04_F3.jpg

Fig. 3

Graphical comparison results of thermal stress

Table 3.

Thermal stress (MPa) computation comparison results

Contents	20°C	10°C	0°C	-2°C	-6°C	-10°C	-20°C	-30°C	-40°C
SRRAP	0.0007	0.0082	0.0448	0.0617	0.1156	0.2129	0.8820	2.9256	7.2946
DRRAP	0.0008	0.0088	0.0476	0.0656	0.1231	0.2271	0.9506	3.1801	7.9021
Diff.	0.0001	0.0006	0.0028	0.0039	0.0074	0.0142	0.0686	0.2545	0.6074

Diff. = DRRAP - SRRAP

Therefore, it can be said that there is a possibility that applying DRRAP mixtures on actual asphalt pavement work. However more extensive experimental works with various mathematical analysis works are needed to further verify findings in this paper.

5. Summary and conclusion

In this paper, low temperature performance evaluation of DRRAP mixture was considered. As an experimental work, BBR mixture creep testing was considered and thermal stress was computed then compared by means of simple Power-law transformation function. No significant differences of thermal stress results between SRRAP and DRRAP mixtures were found which means a possibility of using DRRAP on actual asphalt pavement work could be derived.

However, only one asphalt mixture sample was considered in this paper. Therefore, more extensive laboratory works with various mathematical analysis procedures are strongly needed to further verify findings in this paper as a future research.

References

Barisic, I., Grubesa, I.N. and Kutuzovic, B.H. (2017). “Multidisciplinary approach to the environmental impact of steel slag reused in road construction”, Road Materials and Pavement Design, 18(4), pp. 897-912. doi: 10.1080/14680629.2016.1197143. 10.1080/14680629.2016.1197143

Heneash, U. (2013). Effect of the repeated recycling on hot mix asphalt properties. Ph.D. thesis, University of Nottingham, U.K.

Kareem, A.I., Nikraz, H. and Asadi, H. (2019). “Performance of hot-mix asphalt produced with double coated recycled concrete aggregates”, Construction and Building Materials, 205, pp. 425-433. doi: 10.1016/j.conbuildmat.2019.02.023. 10.1016/j.conbuildmat.2019.02.023

Marasteanu, M.O., Velasquez, R.A., Falchetto, A.C. and Zofka, A. (2009). Development of a simple test to determine the low temperature creep compliance of asphalt mixtures, NCHRP-133 Final Report

MOLIT (2017). A specification for production, management and construction of hot mix asphalt material, Ministry of Land, Infrastructure and Transport-South Korea.

Moon, K.H., Falchetto, A.C., Marasteanu, M. and Turos, M. (2014). “Using recycled asphalt materials as an alternative material source in asphalt pavements”, KSCE Journal of Civil Engineering, 18(1), pp. 149-159. doi: 10.1007/s12205-014-0211-1. 10.1007/s12205-014-0211-1

Moon, K.H., Falchetto, A.C., Marasteanu, M.O. and Wistuba, M.P. (2017). “Low temperature rheological properties of asphalt mixtures containing different recycled asphalt materials”, International Journal of Pavement Research and Technology, 10(1), pp. 84-97. doi: 10.1016/j.ijprt.2016.11.007. 10.1016/j.ijprt.2016.11.007

Moon, K.H., Marasteanu, M.O. and Turos, M. (2013). “Comparison of thermal stresses calculated from asphalt binder and asphalt mixture creep tests”, ASCE-Journal of Materials in Civil Engineering, 25(8), pp. 1059-1067. doi: 10.1061/(ASCE)MT.1943-5533.0000651. 10.1061/(ASCE)MT.1943-5533.0000651

Ossa, A., Garcia, J.L. and Votero, E. (2016). “Use of recycled construction and demolition waste (CDW) aggregates: a sustainable alternative for the pavement construction industry”, Journal of Cleaner Production, 135, pp. 379-386. doi: 10.1016/j.jclepro.2016.06.088. 10.1016/j.jclepro.2016.06.088

West, R.C. and Willis J.R. (2014). Case studies on successful utilization of reclaimed asphalt pavement and recycled asphalt shingles in asphalt pavements, National Center for Asphalt Technology, Final report 14-06.

Journal of the Korean Asphalt Institute ISSN:2234-0785(Print) 2635-9553(Online) 한국아스팔트학회지

Preview

Performance evaluation of Double Recycled Reclaimed Asphalt Pavement (DRRAP) at low temperature

ABSTRACT

MAIN

Table 1.

prepared asphalt mixtures in this paper

Fig. 1

prepared asphalt mixtures (SRRAP and DRRAP)

Fig. 2

Bending Beam Rheometer (BBR) mixture creep test

Table 2.

Information of BBR mixture testing

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

Fig. 3

Graphical comparison results of thermal stress

Table 3.

Thermal stress (MPa) computation comparison results

References