1. 서 론

시험 데이터를 제한된 조건 밖에서 아스팔트 바인더의 공용성 분석을 위해 기존과 같이 하나의 수학적 모델을 이용하여 예측한 경우 그 결과값의 대표성 및 신뢰성에 있어서 부족함이 발생할 수 있기에 새로운 수학적 모델의 제시를 통해 예측 결과의 광범위한 변동 폭(예: 상한 및 하한값)을 제시할 필요가 있다.

아스팔트 바인더의 특성을 예측하고 분석하기 위해 새로운 수학적 모델을 제안하고자, 기존에 통용되고 인정되어온 시그모이드 함수와 리차즈 함수를 기반으로 하여 새로운 모델식을 제안하고 이에 대한 비교, 검증을 실시하고자 한다. 아스팔트 바인더의 마스터커브 작도를 위해서는 S자 형태의 특성을 보이는 시그모이드 함수가 사용되는데, 물리적 시험결과 범위를 벗어나는 조건의 결과값을 예측하는 부분에 있어서 하나의 수학적 모델로 얻어진 예측값만을 적용하기에는 아스팔트 바인더의 점탄성 거동 특성을 예측하는 것에 오류가 발생할 수 있다. 따라서, 시그모이드 함수와 이를 기반으로 추가적인 수학적 모델의 개발 및 제안을 통해 물리적 시험 범위를 벗어나는 결과값 예측의 다양화를 현실화 할 수 있으며, 점탄성 특성 변화에 따른 신뢰성 있는 예측 모델을 제안할 수 있을 것으로 기대된다. 본 연구의 목적은 아스팔트 바인더의 점탄성 거동 특성을 분석하고, 물리적으로 시험 가능한 온도 또는 주파수를 벗어난 범위에서 시그모이드 함수 및 리차즈 함수 뿐만 아니라 3가지의 새로운 모델식 또한 점탄성 거동 특성을 분석할 수 있음을 중명하는 것이다.

2. 문헌조사

2.1 시그모이드 함수

아스팔트 바인더는 점탄성 특성으로 인해 시간-온도 중첩이론이 적용된다. 아스팔트 바인더의 마스터커브를 이용하여 다양한 하중, 시간(주파수) 및 시험 온도를 사용하여 시험을 수행한 경우 점탄성 재료를 비교할 수 있다. 아스팔트 바인더의 점탄성 거동을 설명하는데 마스터커브를 구성하기 위한 시그모이드 함수(Sigmoid function) 적용이 가능한 것이다(Pellinen et al., 2004).

시그모이드 함수는 1937년 Hyman Lumer에 의해 개발되었다(Lumer, 1937; Wilson et al., 1972). 이 함수는 단순선형회귀분석(독립변수의 갯수가 1개)은 목표가 실수값 예측이기 때문에 선형함수 “y = wx + b”를 이용하여 예측한다(예측 변수의 수가 하나인 경우). 하지만 로지스틱 회귀분석에서는 종속변수(y)가 0 또는 1이기 때문에 단순 선형으로는 예측이 불가능하다(Pellinen et al., 2004). 그래서 Odds를 이용하는데 Odds는 식 (1)과 같이 정의된다. 확률 p가 주어져 있을 때

로 정의한다. 확률 p의 범위가 (0, 1)이라면 Odds(p)의 범위는 (0, ∞)이 된다. Odds에 로그함수를 취한 log(Odds(p))은 범위가 (-∞, ∞)이 된다. 즉, 범위가 실수 전체이다. log(Odds(p))의 범위가 실수이므로 이 값에 대한 선형회귀분석을 하는 것은 의미가 있다(Pellinen et al., 2004; Wilson et al., 1972; Lumer, 1937).

식 (2)와 같이 선형회귀분석을 실시해서 w와 b를 얻을 수 있다. 위 식을 p로 정리하면 식 (3)과 같이 얻을 수 있고 이 식이 시그모이드이다(Pellinen et al., 2004; Wilson et al., 1972; Lumer, 1937).

다항의 함수는 구간분할접근법을 사용하여 아스팔트 바인더 시험데이터를 이동시키는데 사용되어왔다. 그러나 극저온 및 극고온에서는 데이터 범위를 벗어나 합리적인 모듈러스 값 예측이 어렵기 때문에 단일 다항식 모델을 전체 마스터 곡선을 작도하기에는 부족함이 있다. 이 문제를 피하기위해 -18°C에서 55°C까지의 온도에서 얻은 테스트 데이터에 적합한 새로운 기능 형태인 시그모이드 함수가 고안되었다(Huang et al., 1993; Pellinen et al., 2004).

아스팔트 점탄성 재료에서 점탄성 거동특성 분석은 시간 온도 중첩 이론을 근거로 모델링하는 데 일반적으로 사용되는 방법은 세가지로, 로그선형 방정식(log-linear), 아레니우스 방정식(Arrhenius) 및 윌리엄스 랜델 및 페리(Williams Landel and Ferry, WLF) 방정식이다. 아레니우스 및 WLF 방정식은 아스팔트 바인더에 대한 a(T) 및 온도와의 관계를 분석하기 위해 사용되었으며, 아레니우스 및 로그선형 방정식은 아스팔트 혼합물의 점탄성 거동특성 분석에 사용되었다(Francken et al., 1998; Pellinen et al., 2004).

아스팔트 바인더의 거동특성 분석을 위해 주어지는 데이터는 저온에서 중간온도로 제한적이다. 그러므로 시간-중첩원리를 근거로 하여 시험데이터를 일정식을 통해 이동시킬 수 있으며 이를 Shifting Techniques라 한다(Rogue et al., 1992; Christensen et al., 1998; Pellinen et al., 2004).

마스터커브 작도를 통해 극저온 또는 고온 데이터를 예측할 수 있게 됨에 따라 다항 이동함수는 아스팔트 바인더의 거동특성 분석에 이용되어지고 있다(Francken et al., 1998).

시험데이터를 이동시켜 마스터커브를 작도하기 이전까지는 시험 데이터에 대한 다항식 함수를 온도 구간별로 쪼개서 복합전단계수를 계산하기도 하였고, 시험데이터를 기준온도의 범위로 이동하기 위해 구간을 나눠서 함수를 재정의 하는 cubic spline method를 추가하기도 하였다(Gordon et al., 1994).

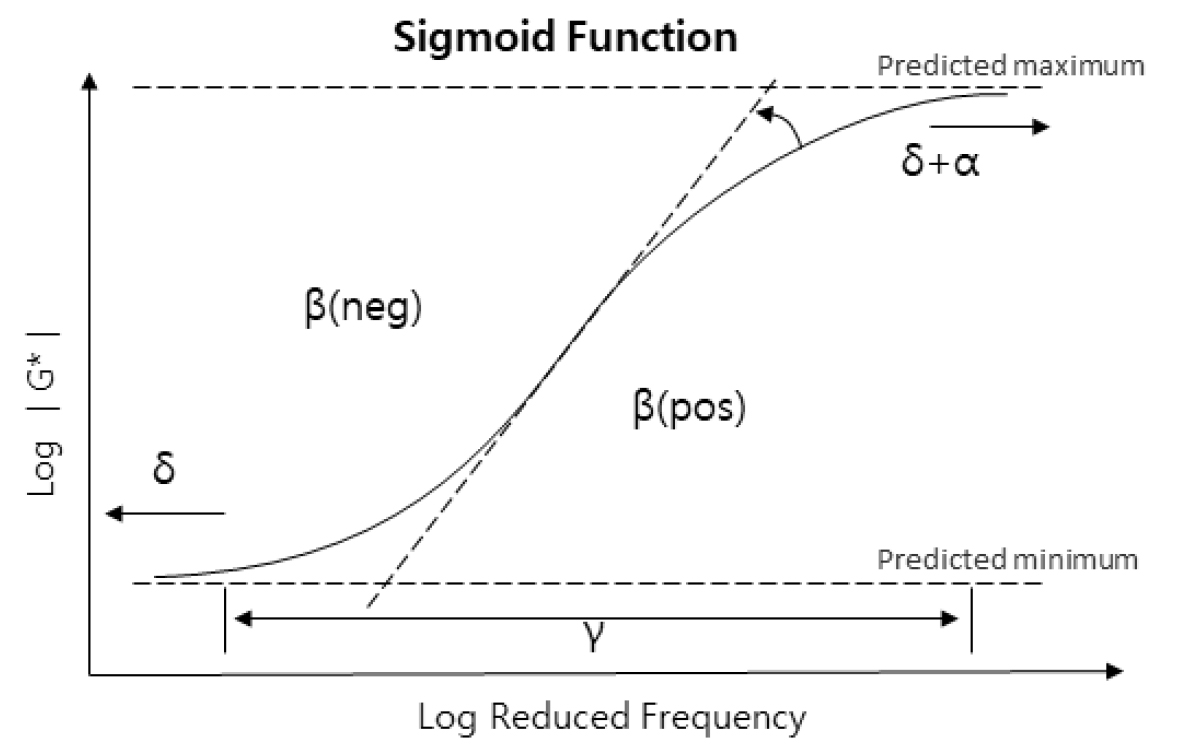
앞서 언급한바와 같이, 시그모이드 함수는 극저온 및 극고온에서의 데이터 범위를 벗어난 구역에서의 아스팔트 바인더의 성능을 예측하기 위해 고안된 방법이며, 식 (4)와 같다. Fig. 1은 시그모이드 함수의 원리를 설명하는 것으로 |G*|는 복합전단계수(Complex Shear Modulus), w는 주파수(frequency, [rad/s]), wr는 기준온도에서 하중재하 시의 수축 주파수(reduced frequency, [rad/s]), aT는 시간-온도 중첩원리에 기반한 온도의 함수로써 전이함수(Shift Factor), δ는 복합전단계수의 최소값(minimum modulus value), α는 복합전단계수의 최대값(Range of modulus values), β는 S모형의 기울기를 관할하는 형상함수(shape parameters), γ는 양쪽 변곡점간의 거리를 관할하는 형상함수(shape parameters)다(Pellinen et al., 2004).

식 (4)는 |G*(w)|에 대하여 작도된 마스터커브의 좌우측이 대칭 모양을 제공하는 표준 로그 함수다(Yang et al., 2014; Podolsky et al., 2018).

Fig. 1.

Principle of Sigmoid Function

2.2 리차즈 함수

리차즈 함수(Richards Function)는 기존 시그모이드 함수 대비 더 유연적인 함수가 될 수 있도록 독립변수를 추가하여 Richards라는 사람에 의해 1959년 개발되었다(Richards et al., 1959; Patwardhan et al., 2018).

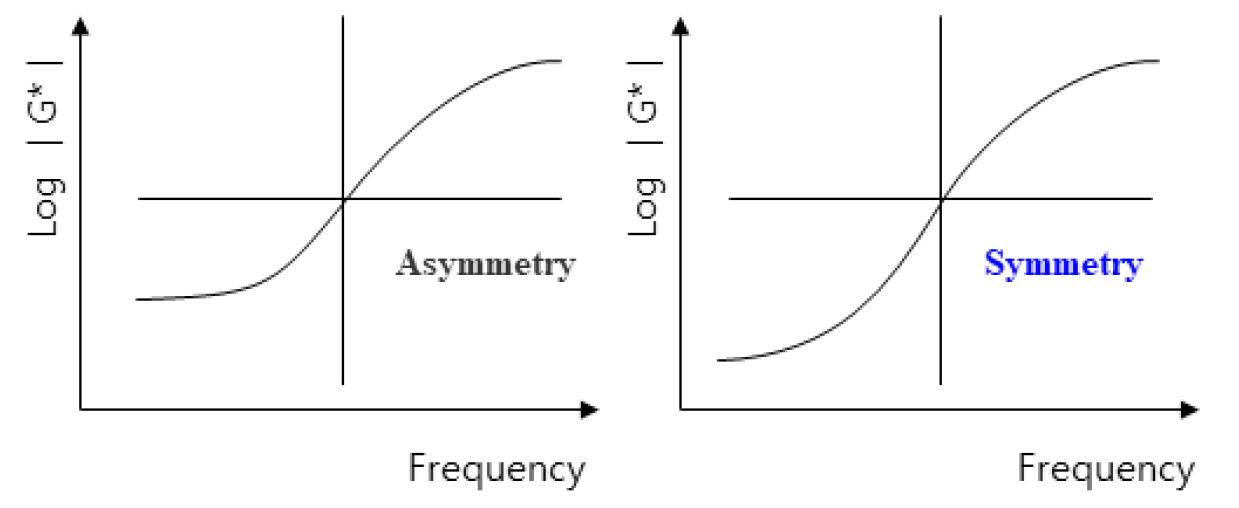
기존의 시그모이드 함수는 아스팔트 바인더 등을 실험하는 경우 |G*(w)| 결과는 불규칙한 이질적인 특성으로 인해 비대칭 패턴을 나타내는 경우가 있었다(Richards et al., 1959; Patwardhan et al., 2018). 리차즈 함수는 기존 시그모이드 함수를 수정한 S자형 함수로 Fig. 2와 같이 |G*(w)|의 비대칭 모형을 보완할 수 있는 독립변수를 추가하여 좀 더 매끄러운 예측이 가능할 수 있도록 도입되었으며 식 (5)와 같다(Yang et al., 1978; Rowe et al., 2008; Moon et al., 2020).

여기서 λ는 함수의 비대칭 모양을 보완하기 위한 독립변수다. 식 (5)도 식 (4)와 마찬가지로 AASHTO Ware-Pavement 프로그램에서 복합전단계수 데이터에 대한 대체옵션으로 사용된다(Yang et al., 1978; Rowe et al., 2008; Cannone et al., 2021).

Fig. 2.

Principle of Richard Function

3. 수학적 모델링 개발

3.1 수학적 모델링 기본개요 Part Ⅰ: 최소자승법

최소자승법(Method of least squares regression)은 어떤 계(데이터)의 해방정식(오차를 최소화하는 직선)을 근사적으로 구하는 방법으로, 근사적으로 구하려는 해와 실제 해의 오차의 제곱의 합이 최소가 되는 해를 구하는 방법이다. 이 방법은 값을 정확하게 측정할 수 없는 경우에 유용하게 사용될 수 있으며, 특히 그 계의 방정식이 어떤 형태인지를 알고 있을 때 방정식의 상수값들을 추정하는 데에 사용된다.

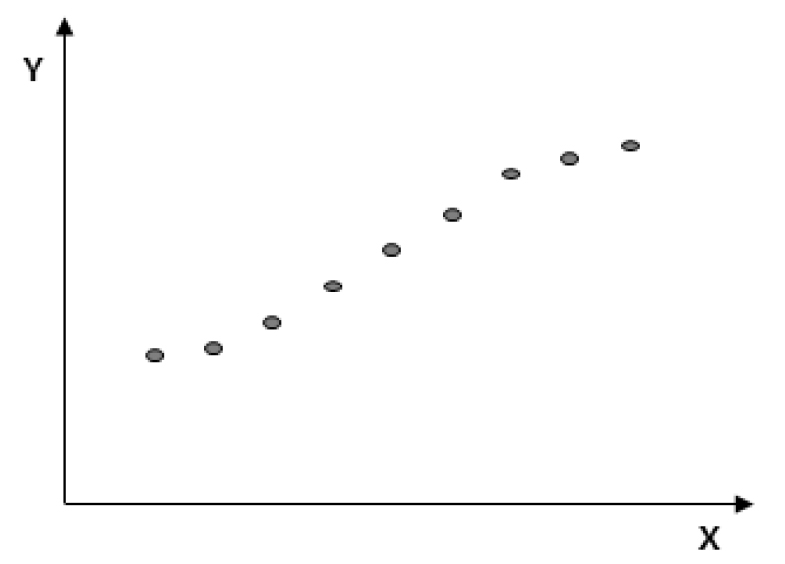
일반적으로 어떤 실험을 할 때, Fig. 3과 같이 독립변수 X를 변경해가며 그에 따른 실험값 Y의 값을 얻는다. 실험을 N회 반복하여 (x1,y1),(x2,y2),...(xn,yn)의 데이터를 확보했을 때, 이 수많은 데이터는 일정한 규칙성을 갖지 못한다면, 이 실험은 아무런 의미가 없게 된다. 따라서, 데이터들의 유용성을 판단하기 위하여 두 변수간에 상관관계가 있는지, 어떤 관계가 있는지 찾아볼 수 있어야 하고, 이는 함수로 표현할 수 있어야 한다.

Fig. 3.

The principle of least squares regression (1)

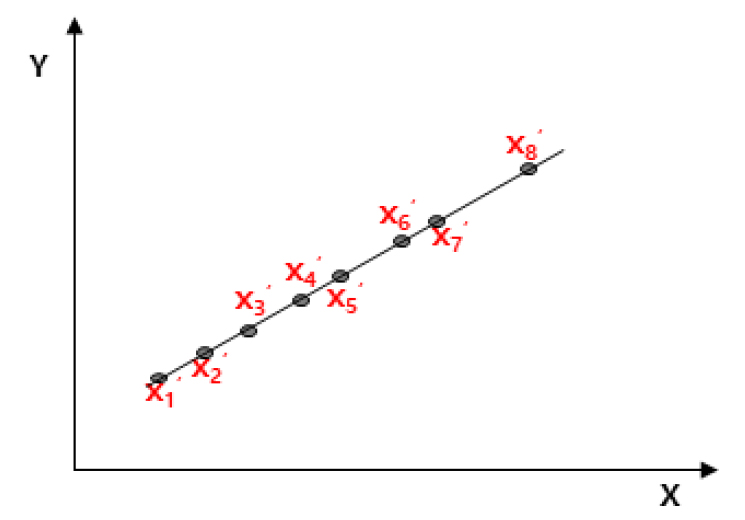
N번 측정한 측정값 y1,y2,...yn이 x1,x2,...xn의 함수 y=f(x)일 것으로 추정할 수 있을 때, Fig. 4와 같이 이를 측정한 값들의 관계에 가장 적합한 함수 y=f(x)의 측정값 yi와 함수값 f(xi)의 차이를 제곱한 것의 합 ∑i=1n(yi-f(xi))2 이 최소가 되도록 함수 y=f(x)를 구하는 것이 최소자승법이다.

Fig. 4.

The principle of least squares regression (2)

이는 Fig. 5와 같이 (측정값-함수값)2의 합이 최소가 되는 직선의 그래프를 찾는 것이다.

다만, 최소자승법(Least Square Method) 활용 시, 그 한계도 잘 알고 있어야한다. 최소자승법은 데이터 중에 보통 outlier(정상적인 데이터 분포에서 동떨어진 데이터)라고 불리는 규칙성 없는 데이터가 존재하는 경우 적용하기 힘든 방법이다. 그 이유는 최소자승법은 전체 데이터의 (측정값-함수값)2의 합을 최소화하기 때문에 outlier와의 차이도 같이 줄이려고 하다보면 전혀 엉뚱한(잘못된) 근사 결과를 낼 수 있기 때문이다. 따라서, outlier가 존재하는 경우에는 RANSAC, LMedS, M-estimator 등과 같은 보완이 가능한 파라미터 추정 방법을 사용해야 한다.

Fig. 5.

The principle of least squares regression (3)

3.2 수학적 모델링 기본개요 Part Ⅱ: 마스터커브 구축

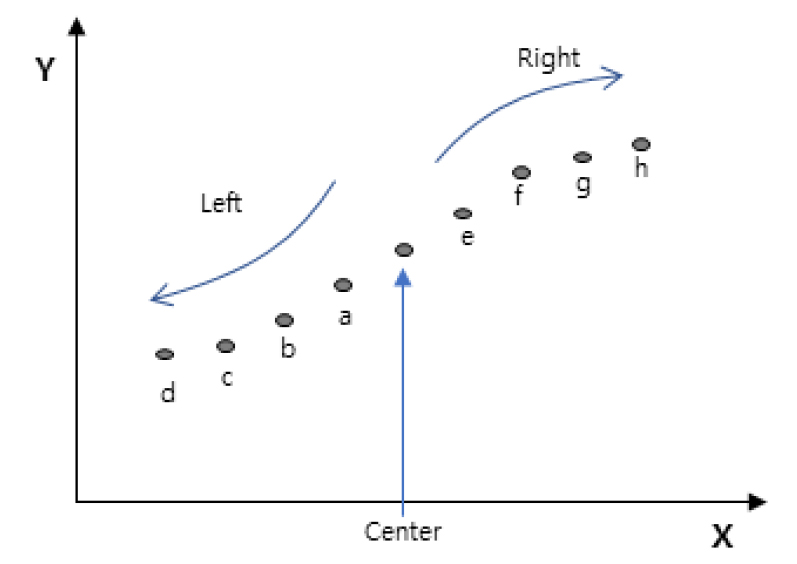
복합전단계수를 평가하고 예측하기 위하여 마스터커브를 작도한다. 수학적 모델에 의해 예측된 극한영역(고온 및 저온)에서의 복합전단계수(Y축)를 그래프로 Fig. 6과 같이 나타낼 수 있다.

Fig. 6.

Construct master curve (1)

최소자승법에 의해 데이터의 에러가 최소화될 수 있도록 보정단계를 거친다. 그 과정은 식 (6), (7), (8)을 따르며 Fig. 7을 참고하여야 한다.

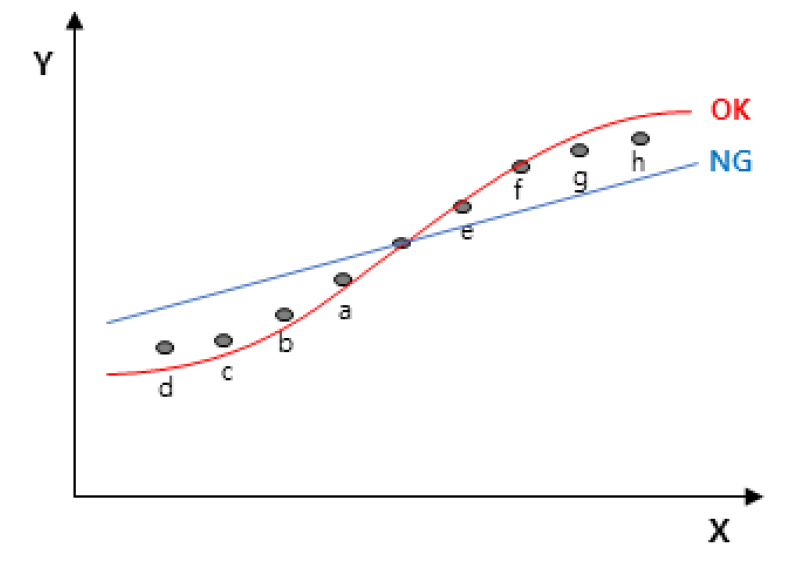
Fig. 8와 같이 마스터커브를 작도할 수 있으며, 오차 보정이 제대로 안되는 경우에는 S자 모형 곡선이 아닌 직선으로 그래프가 그려질 수 있음을 고려해야한다. 그러므로 정확한 S자 모형의 그래프를 얻기 위해 정확한 함수의 모델링이 중요하다.

Fig. 7.

Construct master curve (2)

Fig. 8.

Construct master curve (3)

3.3 복합전단계수 수학적 모델링 제안

Frequency Sweep Test를 통해 각각의 다른 주파수 및 온도조건에 따른 복합전단계수(G*)를 계산하였고, 실험한 조건인 10°C보다 낮은 온도와 60°C보다 높은 조건에서 복합전단계수값을 예측하기 위해 마스터커브를 작성하고 데이터를 확장한다. 마스터커브를 작성함에 있어, 현재 아스팔트 바인더 복합전단계수 분석 및 포장단면구조설계에 광범위하게 적용되는 시그모이드 함수(S 자형 함수)를 적용하였고, 이번 연구에서는 앞글자를 따서 SF하고 명기하였다(Sigmoid Function: SF, Model 1)(Pellinen et al., 2004; Moon et al., 2020).

Model 1(SF)은 아래 식 (9)와 같다.

여기서, G* = 복합전단계수,

δ = 복합전단계수의 최소값

α = 적정 복합전단계수값(δ+α = 최대 탄선계수)

β, γ = 적정 독립변수

ξ = 주파수[rad/s]

f = 최소 주파수[rad/s]

aT = 위상각

하나의 수학적 모델을 이용하여 예측한 경우 그 결과 값의 대표성 및 신뢰성에 있어서 부족함이 발생할 수 있기에 새로운 수학적 모델의 제시를 통해 예측 결과의 광범위한 변동 폭(예: 상한 및 하한값)을 제시할 필요가 있다.

Model 1(SF)의 예측력에 있어 예측 민감도를 높이고자 리차즈 함수라 하는 변형된 시그모이드 함수(S 자형 함수)를 적용하였다(Yang et al., 1978; Rowe et al., 2008; Cannone et al., 2021).

이 모델은 곱의 요소를 추가하여 계수의 변화를 시도한 것으로 추가적인 모델을 제시하는데 방향성을 제시하였으며, 독립변수 람다(λ)를 분자에 곱하고 분모에 제곱하였으므로 본 연구에서는 Model 2(Sigmoid function with Multiple factor : SM)로 정한다.

Model 2(SM)의 구성은 아래 식 (10)과 같다.

여기서, λ = 추가 독립변수

Model 2와 유사 맥락으로 합의 요소를 고려하여 계수의 변화 및 예측 결과값의 민감도 제고를 위해 독립변수 람다(λ)를 분자에 더하고 분모의 제곱에 더하여 새로이 Model 3(Sigmoid function with Sum factor : SS)를 제안하였다,

Model 3(SS)은 아래 식 (11)과 같다.

Model 2와 3 외에도 합과 곱의 요소를 함께 고려한 계수의 변화를 고려하였고, 그 중 분모에 대한 민감도를 더 고려한 Model 4(Sigmoid function with Sum and Multiple factor considering more Denominator than numerator : SD)를 새로이 제안하였다.

Model 4(SD)은 아래 식 (12)와 같다.

마지막으로, Model 4와 유사하게 합과 곱의 요소를 함께 고려한 계수의 변화를 고려하면서, 그 중 분자에 대한 민감도를 더 고려한 Model 5(Sigmoid function with Sum and Multiple factor considering more Numerator than denominator : SN)를 새로이 제안하였다.

Model 5(SN)은 아래 식 (13)과 같다.

본 연구에서는 총 5개의 수학적 모델(기존:2 및 신규:3)의 제시 및 마스터커브의 작도를 통해 발포제가 첨가 된 중온아스팔트 바인더의 동탄성 거동성을 연속적으로 분석·평가 하고자 하였다.

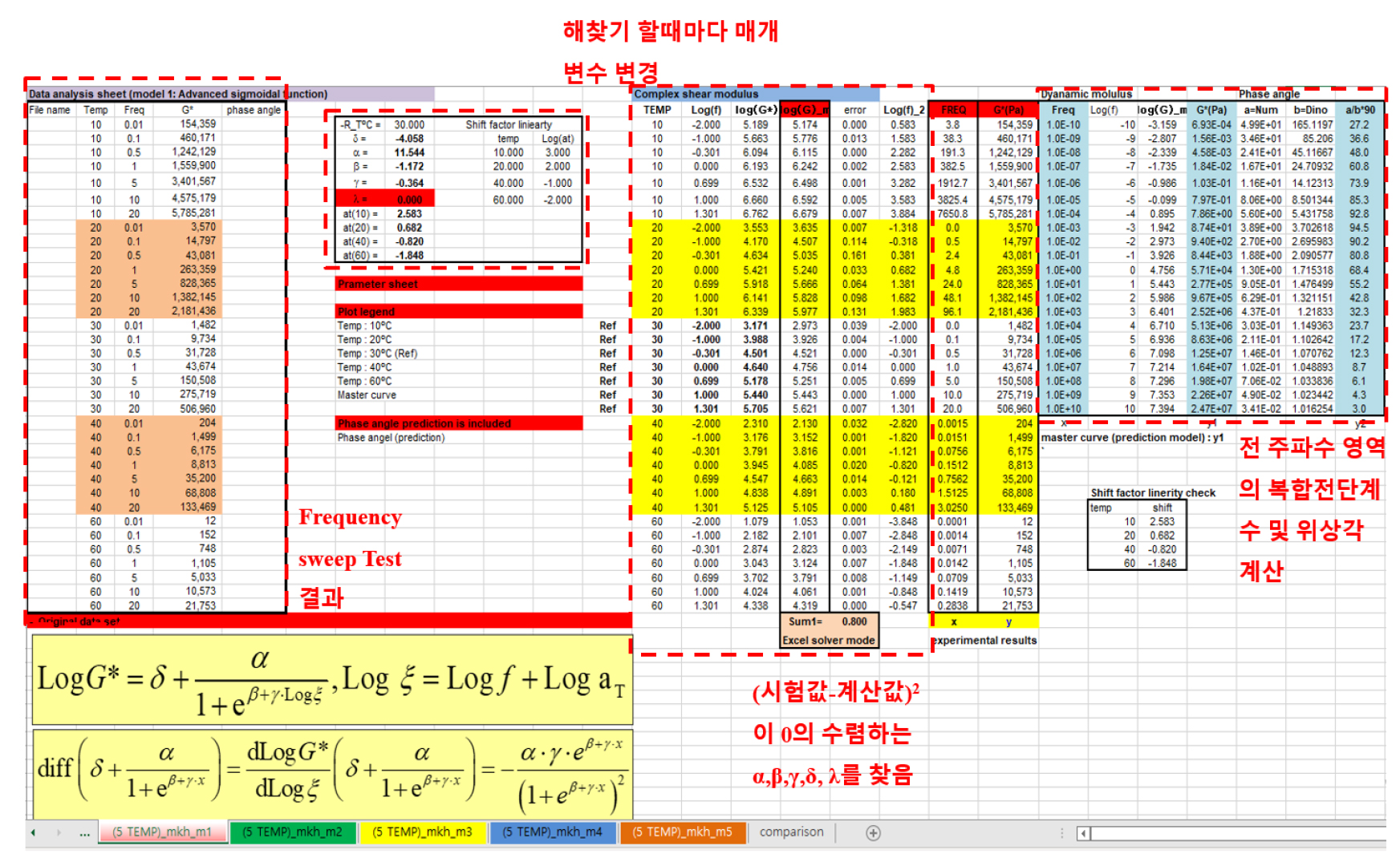
Fig. 9와 같이 최소자승법에 의해 오차의 합이 0에 가까운 해찾기(Microsoft Excel _ Solver 모드)를 이용하여, Frequency sweep Test결과를 바탕으로 오차(시험값-수학적모델에 의한 결과값)의 제곱의 합이 0에 수렴할 수 있도록 반복하였다.

Fig. 9.

Microsoft Excel Solver Mode sample

4. 수학적 모델링의 검증

정리된 오차를 토대로 확인 시 리차즈 함수(Model 2)는 시그모이드 함수(Model 1)보다 정량적 개선사항은 없는 것으로 나타났다. 단, 1937년 발표 후 22년(1959년)만에 Oxford journals(Oxford University Press)에 실린 SCI논문이며 기존모델의 비대칭성을 보완한다는 의미에서 새로운 모델로 인정되었다. 새로 제안된 Model은 추가적인 실험을 통해 다양한 검증을 필요로 하나, S자 모형은 뚜렷하게 나타냄을 확인하였다.

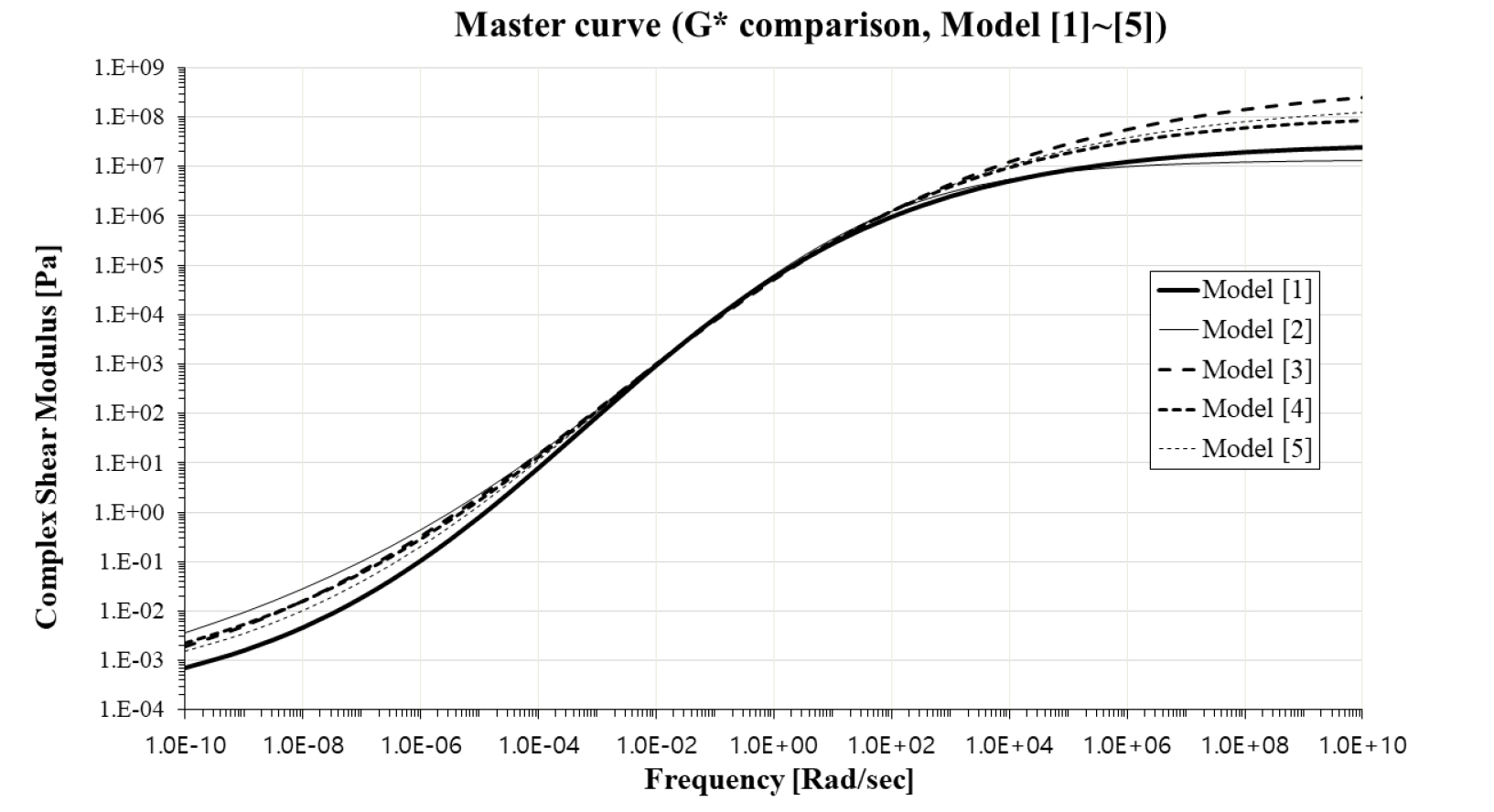
총 5개의 모델식을 통해 시험 가능범위 외에서의 예측범위가 설정될 수 있었다. 하나의 식으로 물리적 시험범위를 벗어나는 범위에서 아스팔트 바인더의 성능을 예측할 경우 하나의 값으로 수렴하는 값이 무조건 맞는 결과로 인정할 수 밖에 없는 일반화의 오류에 대하여 총 5개의 수학적 모델식이 수렴하는 결과값 중 가장 높은 값을 상한, 가장 낮은 값을 하한으로 하여 예측값의 결과를 범위로 설정함으로써 보다 신뢰성있는 결과를 예측할 수 있을 것으로 기대할 수 있다.

5. 결 론

새로운 수학식 개발을 위해 리차즈 함수와 마찬가지로 람다(λ) 파라미터를 도입하였다. 기존 시그모이드 함수의 비대칭적인 한계를 보완하고, 온도 변이영역(마스터커브의 변곡점)에서의 예측력 및 민감도를 향상시킬 수 있다.

초기 수학적 모델 프로토타입을 약 50여개 만들어 적용성을 검토하는 단계를 거쳤다. 마이크로소프트 엑셀 솔버모드(Microsoft Excel _ Solver Mode)를 이용하여 최소자승법을 이용한 피팅작업을 반복하는데 긴 시간이 필요했다. 민감도가 달라지며 S자 모형이 이상해지고, 같은 모델인데도 어떤 시료는 되고, 또 어떤 시료는 안되고, 저온구간은 S모형인데 고온구간에선 직선이 되는 등 많은 시행착오를 겪게 되었고, 다수의 수학적 모델식 중에 단 3개만 원만한 S모형이 가능하였다.

실험한 조건인 10°C보다 낮은 온도와 60°C보다 높은 조건에서 복합전단계수를 예측하기 위해 2개의 기존 및 3개의 신규 제안된 수학적 모델에 의해 마스터커브를 작도하여 데이터를 확장하였다. 근사적으로 구하려는 해와 실제 해의 오차의 제곱의 합이 최소가 되는 해를 구하는 방법인 최소자승법에 의해 데이터의 에러가 최소화될 수 있도록 보정단계를 거치고, 각각의 모델식은 실험이 실행된 온도 또는 주파수에서는 그래프의 위치가 같으나 극한영역인 극고온과 극저온에서는 다소 다른 모양을 이룬다. 단, 모든 마스터커브는 S자 모형의 곡선을 정확하게 이루어야 한다. 오차 보정이 제대로 안되는 경우에는 S자 모형 곡선이 아닌 직선으로 그래프가 그려질 수 있음을 주의해야 한다. 5개의 신규 및 새로 제안된 수학적 모델식에 의한 그래프는 Fig. 10과 같이 서로 상한(Upper bound), 중간(Middle) 및 하한(Lower bound)값을 제공하여 보다 그 공용성의 변화 경향을 폭넓게 예측할 수 있다.

Fig. 10.

Master Curve of Model 1~5