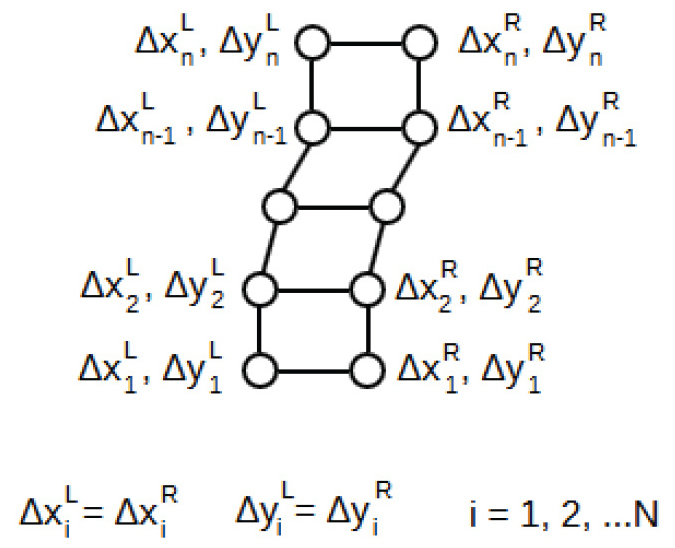1. 서 론
2. 수치해석 해석 조건
2.1 도로 제방 및 경계조건
2.2 입력파
2.3 지반 및 구조물 재료 물성치
3. 수치모델링
3.1 3차원 형상의 2차원 모델링 적용
3.2 각 공법별 수치모델링
4. 수치해석 결과
4.1 파괴기준
4.2 수직 침하 분석 결과
4.3 과잉간극수압비 분석 결과
4.4 수치해석 적용방안
5. 결 론
1. 서 론
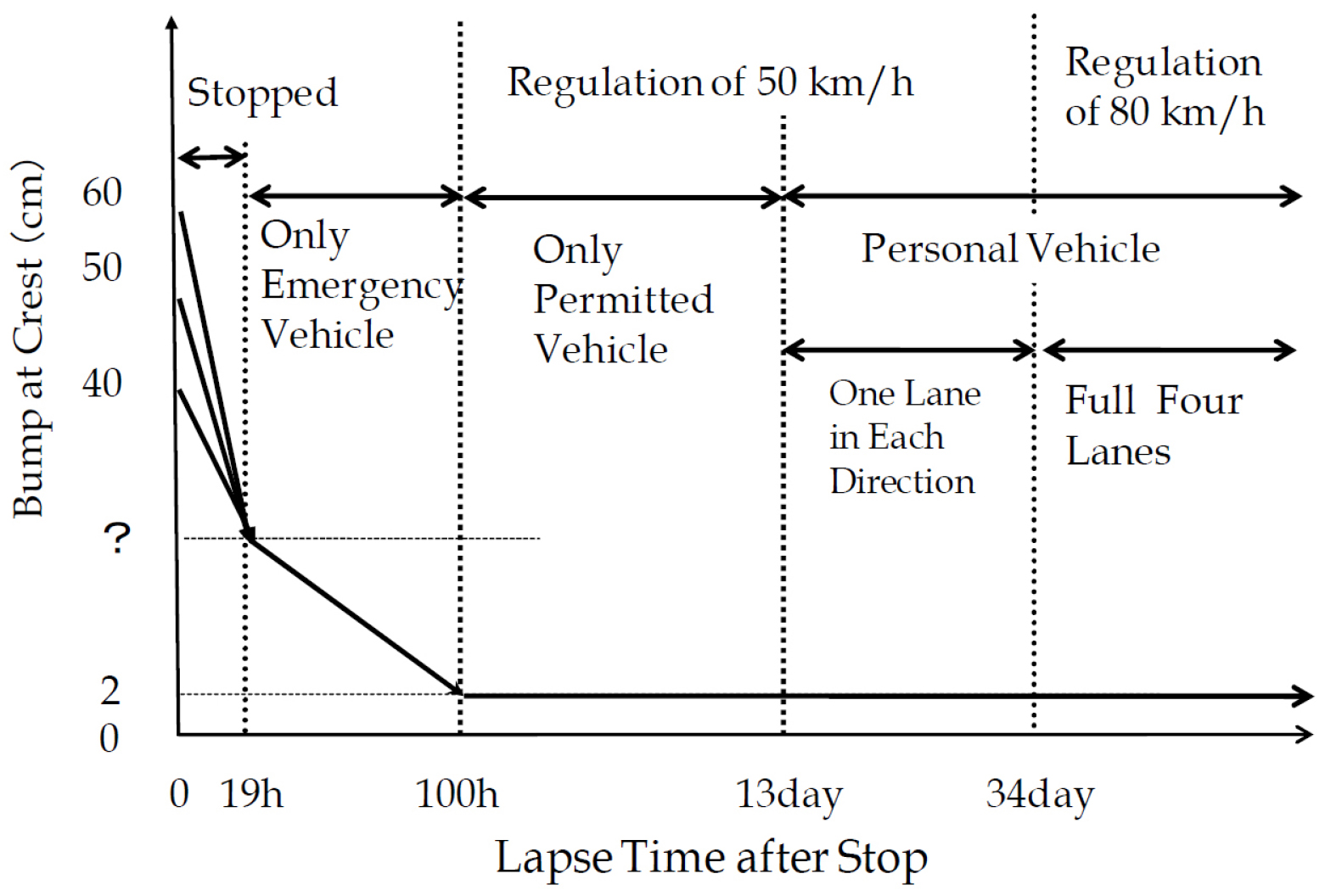
2004년 니가타(Niigata) 지진, 2007년 노토반도(Noto Peninsula) 지진, 그리고 2009년 스루가만(Suruga Bay) 지진 등 많은 지진에서 액상화로 인해 제방이 손상되었다(Tokida, 2012). 국내에서는 2018년에 발생한 포항지진에서 액상화가 발견되었으며, 최근에는 일본 노토반도에서 발생한 지진(2024)으로 인해 액상화가 발생하였다. 이 때, 액상화로 인해 많은 건물의 기초가 파괴되고 지반이 침하되었으며, 안벽, 하천주변, 경사면 등에서 측방유동으로 인해 건물 및 도로가 파괴되는 피해가 발생하였다. 도로 제방의 기초층에서 액상화가 발생하면 제방의 포장층에서 침하가 발생하면서 고속도로의 접근성을 떨어뜨리고, Fig. 1과 같이 피해를 복구하기 위한 구호 시간을 지연시키는 문제가 발생한다. Adalier(1996)는 토사댐과 사면을 다양한 보강을 통한 액상화 대책에 대해 원심모형실험을 수행하여 분석하였으며, Elgamal et al.(2002)는 시트파일에 대해 원심모형실험과 수치해석 비교를 통해 액상화에 대한 효과를 분석하였다. 그리고 Towhata(2006)는 액상화에 대한 다양한 피해를 분석하고, 그에 대한 방지 공법의 중요성을 언급하였다. 그 외에도 많은 연구자들이 모형실험을 이용하여 액상화 방지공법에 대한 많은 연구를 수행하였다(Mohajeri et al., 2004; Sesov et al., 2004; Takahashi et al., 2013). 많은 실험적 연구를 통해 액상화 방지 대책을 분석하고 연구하고 있지만, 각 공법들에 대한 수치해석적 연구는 아직 많이 부족한 실정이다. 본 논문에서는 도로 제방에 적용가능한 다양한 액상화 침하 대책공법을 수치해석적 방법으로 분석하였으며, 다양한 공법의 수치해석 분석을 위한 적용방안을 연구하였다.
2. 수치해석 해석 조건
2.1 도로 제방 및 경계조건
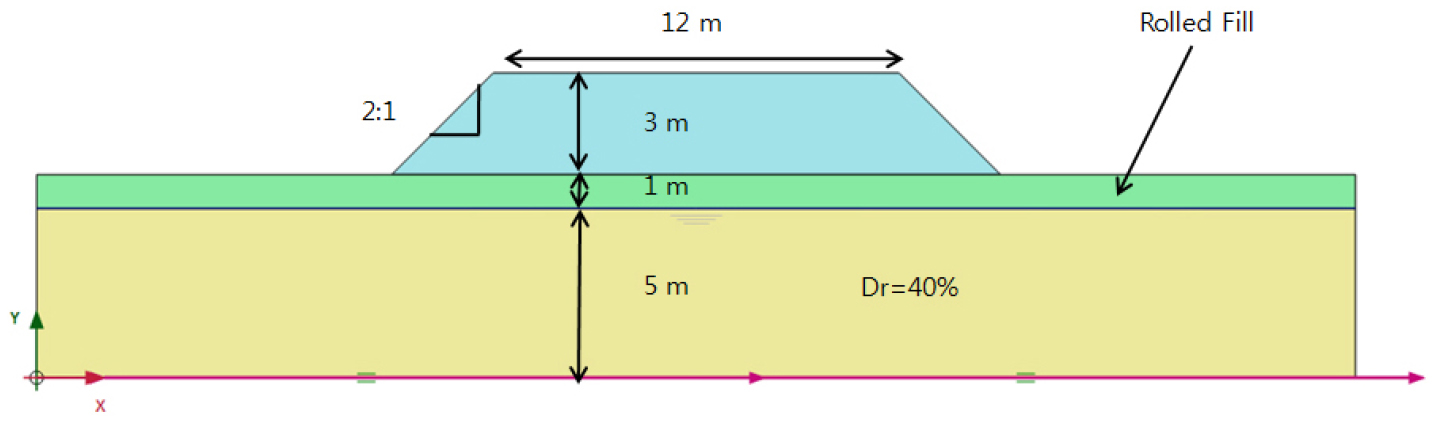
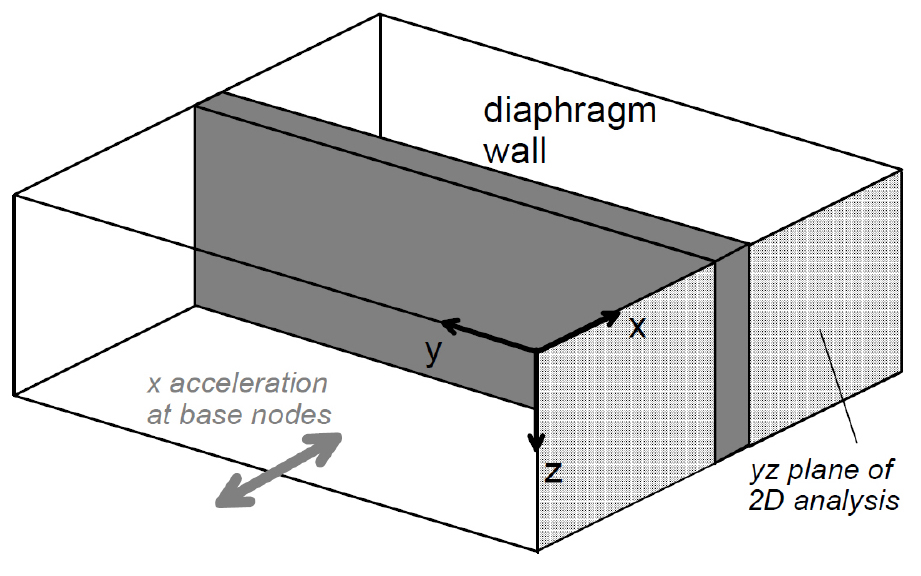
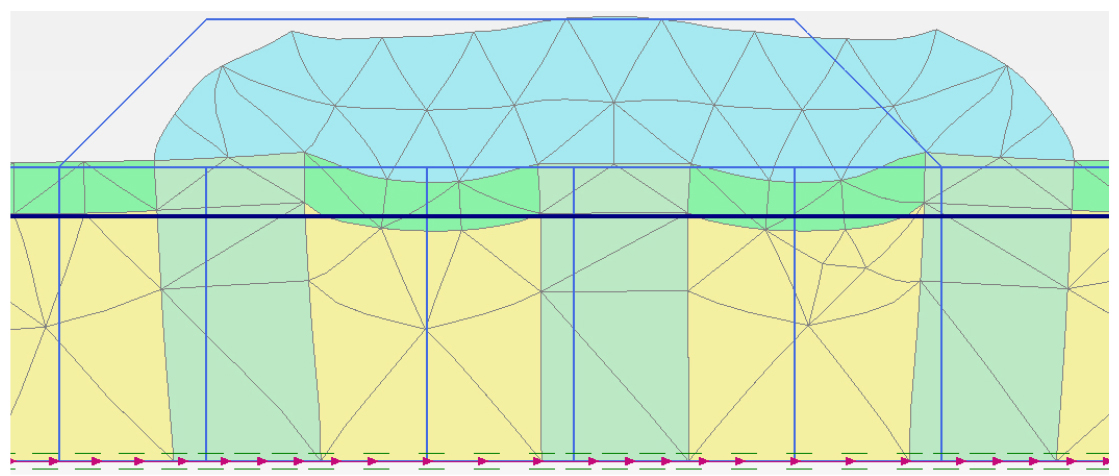
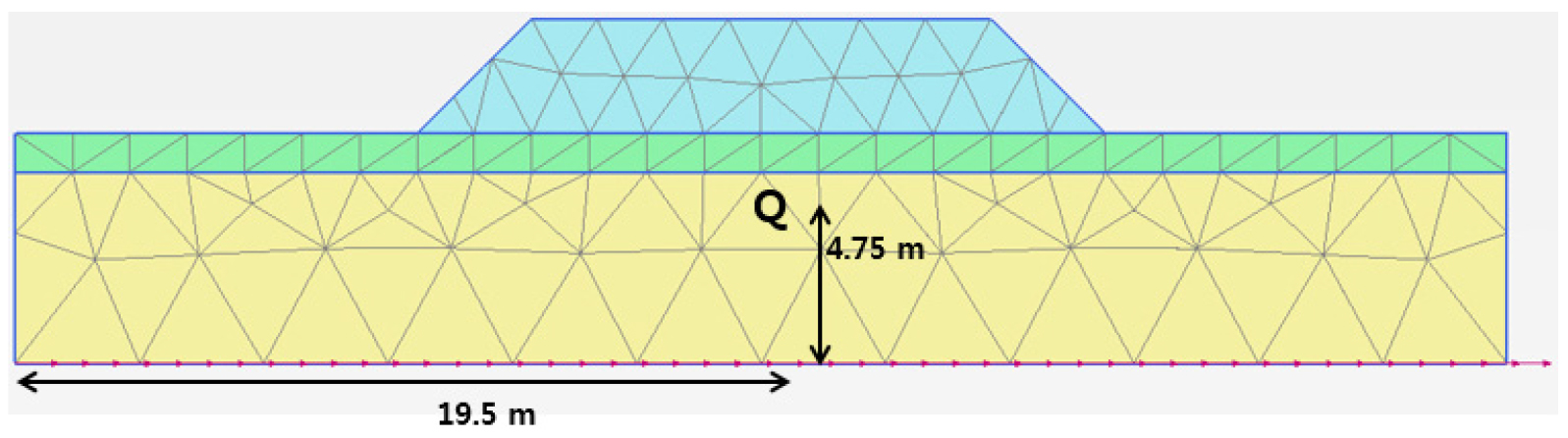
본 연구에서 분석에 사용된 도로 제방의 크기는 도로의 구조・시설 기준에 관한 규칙(국토교통부, 2021)을 바탕으로 2차선 도로에 길어깨의 너비를 고려하여 상단폭을 12m로 결정하였다. 제방의 높이는 3 m이고 사면경사는 2(H):1(V)이다(Fig. 2). 제방은 상대밀도가 40%인 5 m 깊이의 포화된 느슨한 사질토지반과 기저를 이루고 있는 1 m 깊이의 다짐층 위에 조성되어 있다. 향후 모형실험을 수행할 수 있는 점을 고려하여 모델의 측면경계조건은 Zienkiewicz et al.(1989)이 제안한 연결자유도조건(tied degree of freedom)을 사용하였고, 연결자유도조건은 Fig. 3과 같이 좌・우측 모델 경계는 같은 높이를 가지고 있는 노드(node)로 연결되어 있고, 같은 수직 및 수평 침하를 가지는 특징이 있다. 바닥은 수직방향으로 구속되어 있고 수평방향으로 구속되어 있지 않은 기본적인 형태로 설정하였다.
2.2 입력파
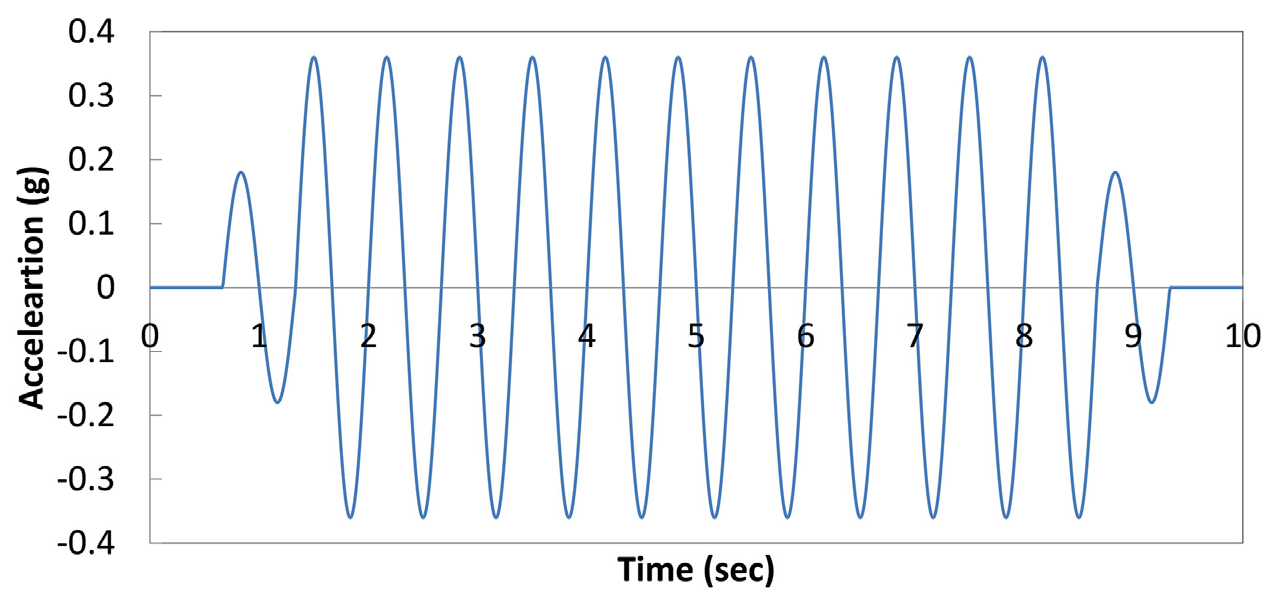
입력파는 1.5 Hz의 주파수와 10초의 지속시간을 가지고 있는 최대입력가속도 0.36 g의 정현파를 사용했다(Fig. 4). 적용된 입력파는 Parra(1996)가 원심 모형실험에 사용했던 최대가속도 0.18 g에 2를 곱하여 액상화 지반에 영향을 줄 수 있도록 적용하였다.
2.3 지반 및 구조물 재료 물성치
2.3.1 지반
본 연구에서 액상화 지반의 구성모델은 UBCSand 모델을 적용하였다. UBCSand 모델은 Puebla et al.(1997)과 Beaty and Byrne(1998)이 기본 수학적 공식을 확립한 모델이다. 이 모델은 지진 시에 발생하는 전단파로 전달되는 전단력으로 인한 지반의 변형을 가장 잘 모사하는 직접단순전단 시험에 기초하고 있으며 흙의 응력-변형률-체적 관계를 계산할 수 있다. 수치해석 모델링을 위한 UBCSand 구성모델의 입력 파라미터를 구하기 위해 상대밀도와 표준관입시험(standard penetration test, SPT) N치(), UBCSand 구성모델의 입력 파라미터 사이의 상관관계를 사용하였다. Meyerhof(1957)는 모래의 상대밀도와 N치의 경험적 관계식을 식 (1)과 같이 제안하였다.
여기서, , 은 유효상재응력이고, 는 대기압이다.
많은 연구자들이 를 다양하게 제안하였지만, 본 연구에서는 Idriss and Boulanger(2008)가 제안한 46을 값으로 사용하였다. Beaty and Byrne(2011)은 깨끗한 모래에서의 N치와 UBCSand 파라미터 사이의 관계식을 제안하였다. 관계식은 아래 식 (2), (3), (4), (5)와 같다.
여기서, 는 탄성전단정수(elastic shear modulus), 는 탄성체적정수(elastic bulk modulus), 는 소성전단정수(plastic shear modulus), 는 최대 마찰각, 는 일정체적(constant volume) 마찰각이다. UBCSand 구성모델에서 와 는 탄성전단계수 G(탄성상태에서의 전단계수)와 소성전단계수 G*(소성상태에서의 전단계수)를 구하기 위해 사용되는 정수이고, 는 탄성체적계수 K(탄성상태에서의 체적계수)를 구하기 위해 사용되는 정수이다.
UBCSand 모델은 탄소성(elastoplastic) 모델이기 때문에 소성과 탄성계수를 처음에 명확하게 정의할 필요가 있다. 이 수치모델에서는 Adalier(1996)와 Elgamal et al.(2002)의 연구를 바탕으로 수치해석을 모델링하였으며, 모래층의 밀도가 40%에서 90%로 증가하도록 동다짐을 하였다. 지반 재료의 물성치는 Tables 1, 2, 3과 같다. 본 연구에서의 파괴의 기본모드는 느슨한 모래기초의 압축으로 인한 제방에서의 침하이다. 이에 하부층은 정교한 구성 모델을 선정하여 모델링하였다. 상부의 제방과 제트 그라우팅에 사용될 그라우팅 플러그는 모아-쿨룽 모델(Mohr-Coulomb model)을 사용했으며, 다짐층은 비선형적인 응력-변형 관계를 나타낼 수 있도록 쌍곡선 모델(hyperbolic model), 액상화 발생 가능성이 있는 하부층은 UBCSand 모델을 3차원 구성방정식으로 확장시켜 액상화 거동을 모사할 수 있는 UBC3D-PLM 모델(Petalas, 2012; Petalas and Galavi, 2013; Tsegaye, 2010)을 사용했다.
Table 1.
Mohr-Coulomb Properties of Embankment
| Parameters | Embankment | Grout Plug |
| Type | Drained | Non-Porous |
| 20 kN/m3 | 17 kN/m3 | |
| 5 kPa | 750 kPa | |
| 30° | 0° | |
| 0.3 | 0.3 | |
| 30 |
Table 2.
Hardening Strain Properties of the Rolled Fill
| Parameters | Rolled Fill |
| 22 kN/m3 | |
| 21 kN/m3 | |
| 124.5 kPa | |
| 25° | |
| 0.2 | |
| 16570 kPa | |
| 16570 kPa | |
| 49710 kPa | |
| 0.6 | |
| 0.8 | |
| 0.9 |
Table 3.
UBC-3D PLM Parameters for Loose and Dense Sand
| Parameters | ||
| 14 kN/m3 | 18 kN/m3 | |
| 13 kN/m3 | 17 kN/m3 | |
| 7.36 | 37.26 | |
| 37.5° | 43.27° | |
| 37.57° | 47.72° | |
| 843.65 | 1447.82 | |
| 590.55 | 1013.47 | |
| 237.10 | 6130.05 | |
| 0.82 | 0.64 |
2.3.2 시트파일 및 스트러트
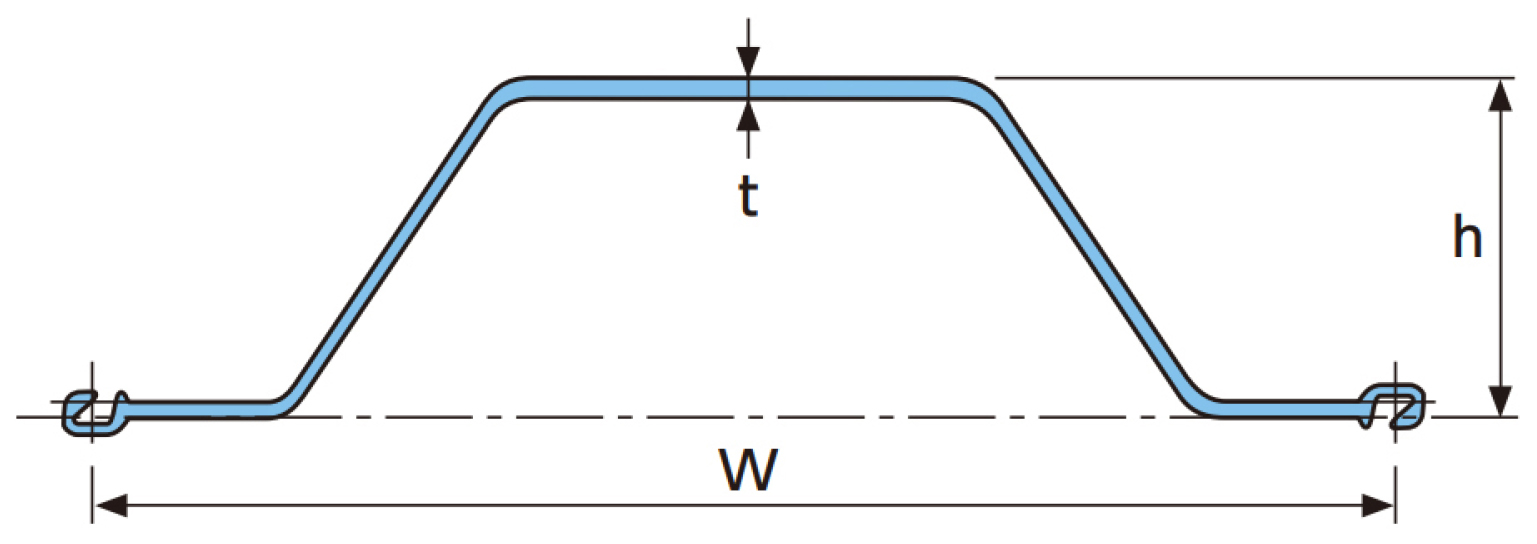
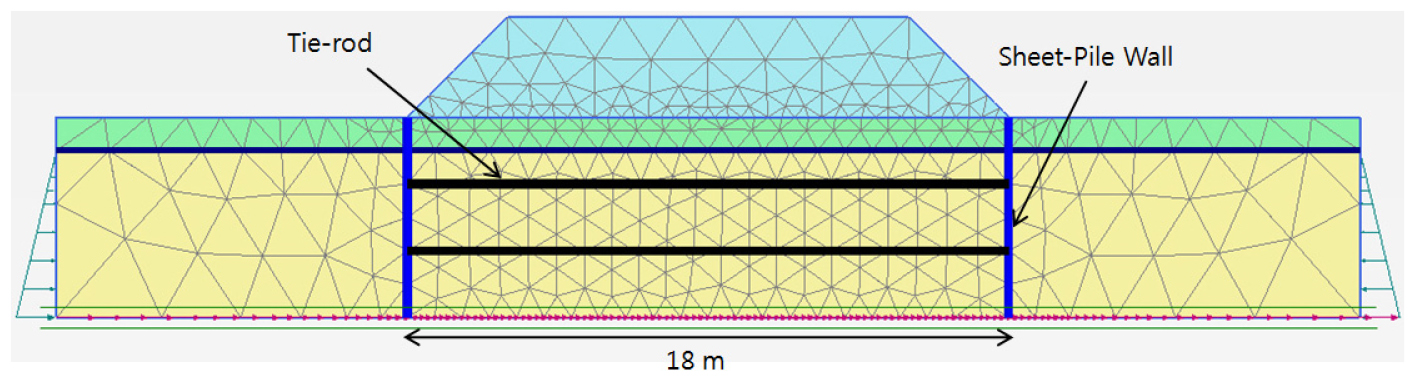
시트파일 모델링은 구조적인 개체 사용이 필요하다. 시트파일은 일본의 스미모트 금속과 일본제철에서 사용하고 있는 NS-SP-50H 단면을 사용하였다. NS-SP-50H 단면은 Fig. 5와 같이 모자 타입(hat type)의 형상을 가지면서 900 mm(W) × 370 mm(h) × 17 mm(t)의 크기를 가지고 있다. 스트러트(strut)은 북미의 철강회사인 Skyline의 #28 Grade 75 threaded bar를 사용하였다. Table 4와 Table 5는 두 가지 재료의 특성을 보여준다. 이 수치모델에서 시트파일은 축방향 하중과 휨(bending)이 가능한 판(plate)으로 모델링하였으며, 스트러트는 오직 축 방향 하중만 전달될 수 있는 앵커로 모델링하였다.
3. 수치모델링
3.1 3차원 형상의 2차원 모델링 적용
액상화 방지 공법을 모델링하기 위해서는 2D 공간(2-Dimension zone, 2D)에서의 2D 모델을 3D 모델처럼 근사적으로 거동할 수 있는지 확인하는 것이 필요하다. 예를 들면, 동다짐, 제트 그라우팅, 그리고 자갈배수 공법의 성능은 기하학적 배치의 수평 거리에 영향을 받는다. 그러나, 이러한 문제의 계산시간 효율성을 높이려면 모델이 2D 환경에 맞춰져야 한다. 이에 본 연구에서는 3D 공간에서 구성된 자갈배수, 벽, 말뚝을 2D 공간에서 모델링한 Papadimitriou et al.(2005; 2007)가 사용했던 방법을 사용하였다. 여기서 3D 기하학적 특성을 변환하는 가장 좋은 방법은 2D와 3D 모델의 단면계수를 동일하게 하는 것이라고 하였다. 이와 관련하여, 개량된 지반 기둥의 수평거리는 지하 연속벽(continuous diaphragm wall)으로 모델링하였고, 이를 통해 3D 조건을 2D 조건으로 변환하였다(Figs. 6~7). 이 개념은 동다짐과 제트 그라우팅에서 찾을 수 있는 개량 기둥에 적용할 수 있다. Papadimitriou et al.(2005)는 식 (6), (7), (8), (9)에 있는 3D와 2D 단면계수를 등가로 사용하면 오차가 가장 작다는 것을 발견했다.
여기서, W는 단면계수이고, 와 는 각각 개량기둥의 직경과 측면거리이다. 식 (8)에서, 은 2D모델의 yz 평면에서의 지하연속벽의 너비와 동일하다. 이런 이유로 1 m 간격으로 이격된 2m의 개량기둥은 2.82 m 두께의 지반 지하연속벽이 계산되었다. 시트파일 방법은 이미 3D 또는 2D의 지하연속벽이기 때문에, 등가방법은 더 이상 필요하지 않았다. 자갈 배수의 3D 모델을 2D 모델로 변환하는 것도 동일한 모델링 원리를 적용하였다.
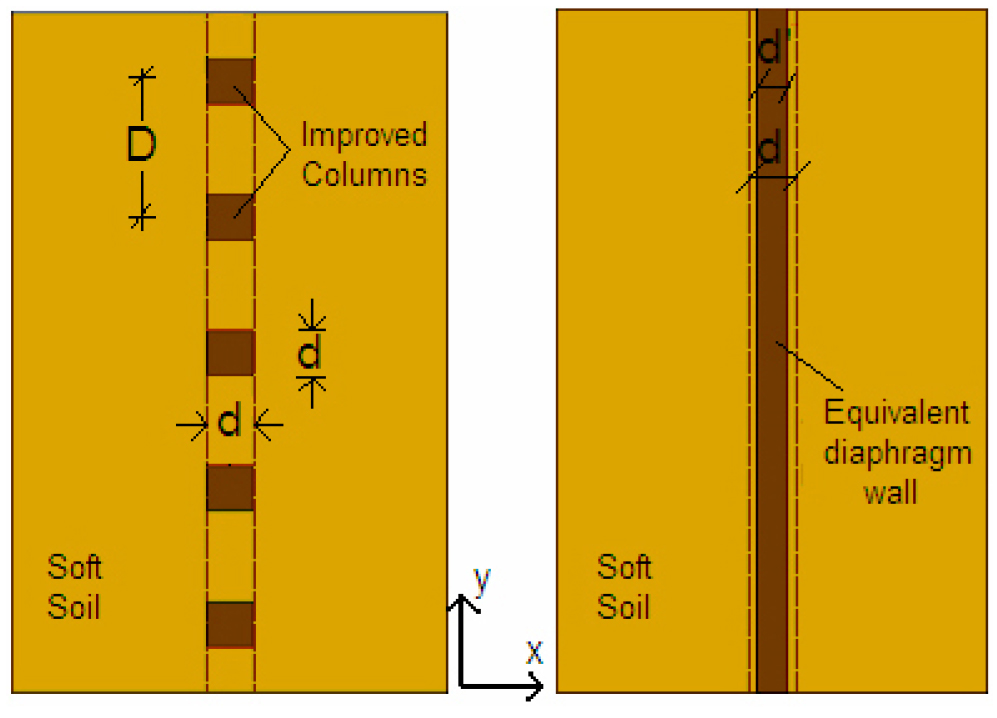
Fig. 6.
Plan View of 3D Soil Improvement Columns Modeled as 2D continuous Diaphragm Wall (Papadimitriou, 2005)
3.2 각 공법별 수치모델링
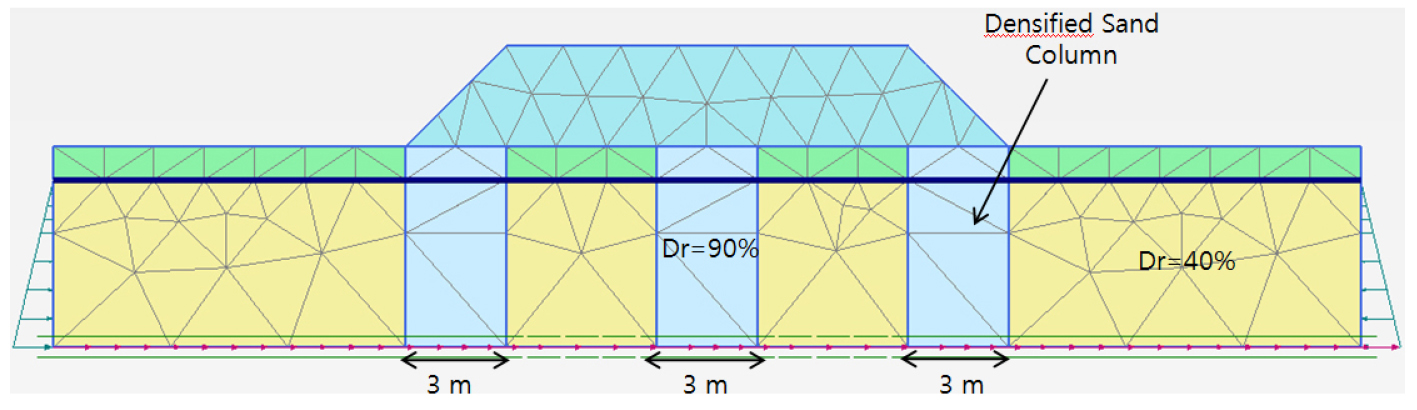
깊은 동다짐(Deep Dynamic Compaction)은 상대밀도가 90%가 되도록 현장모래의 밀도를 증가시키기 위해 해머드롭(hammer drop)을 사용하는 것이다. Adalier(1996)은 실제 현장시험은 상한계(upper bound)가 증가한다는 것을 증명하였다. 조밀한 모래 기둥은 Oshima and Takada(1997)의 영향반경과 Elgamal et al.(2002)의 연구를 참조하여 직경을 3 m로 하였다. 세 개의 기둥은 제방의 양 끝부분과 제방 중심에 위치시켜 모델링하였다. 모델의 단면은 Fig. 8과 같다.
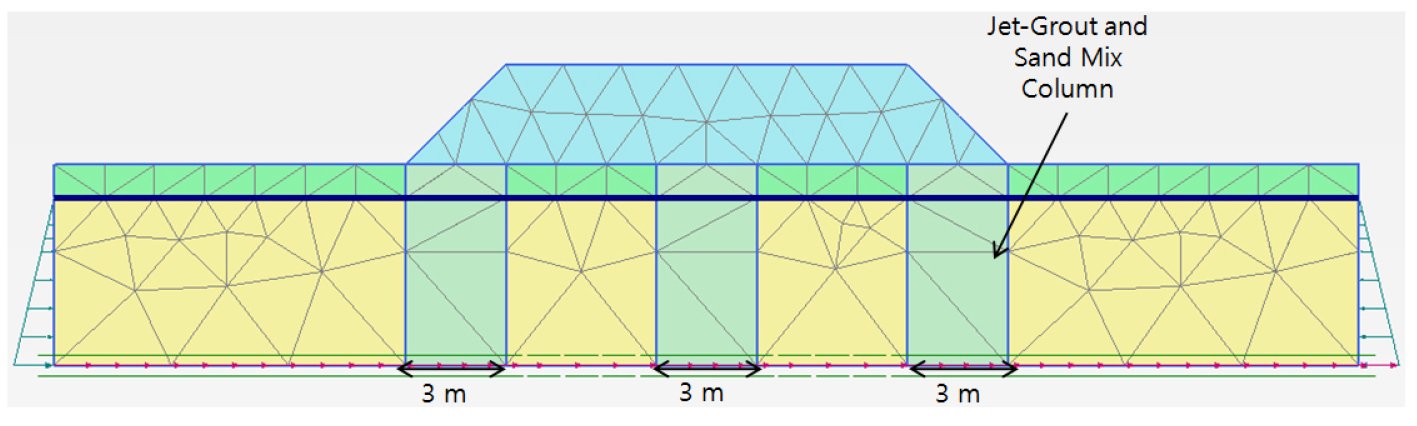
제트 그라우팅은 간극을 채우고 불투성이면서 균질한 혼합물을 만들기 위해 그라우트 플러그(grout plug)를 사용하였다. 간극이 감소하면 과잉간극수압 발생을 억제시키면서 지반의 지지력을 향상시키는 효과가 있다. 기하학적 구조는 깊은 동다짐 모델과 동일한 형태를 가지도록 모델링하였다(Fig. 9). Table 1에서 언급한 그라우트 플러그 물성치는 Plaxis의 제트 그라우트 모델링 작업을 수행한 Chan(2005)의 연구에서 얻었다.
시트파일은 제방의 극한 침하와 측방유동을 막기 위해 밀폐된 지반의 이동을 구속하는 구조적인 개체이다. 시트파일은 갑작스러운 제방에서의 파괴와 급격한 유동 발생을 막기 위해 타이로드(tie-rod)를 이용하여 고정시켰다. 타이로드는 Fig. 10과 같이 설치하였다.
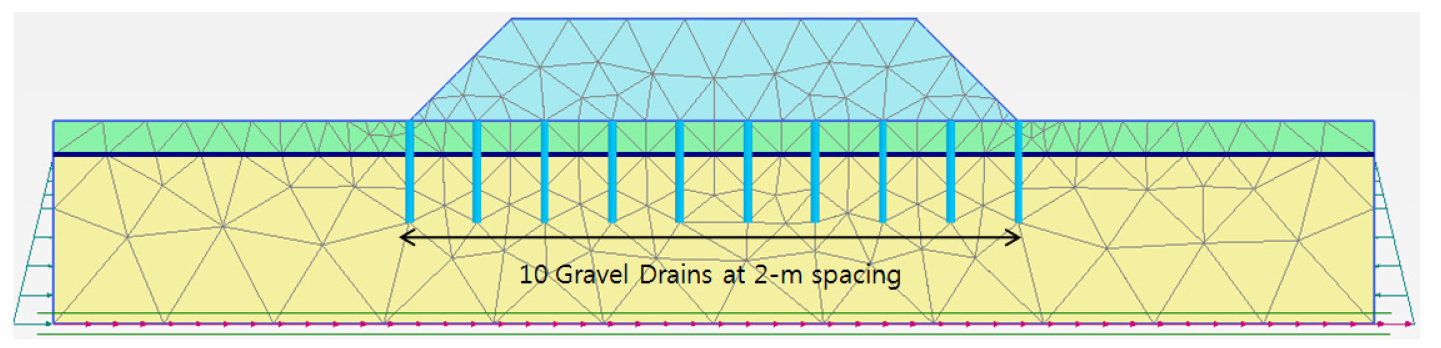
자갈 배수는 간극수가 빠져나갈수 있는 이동로를 제공하여 지반의 과잉간극수압을 완화시키기 위해 사용한다. 과잉간극수압의 빠른 소산은 액상화 발생 및 침하의 억제에 효과가 있다. 이에 자갈에 프로그램 상에서의 배수기능을 적용하였으며, 액상화에 대비하여 자갈 배수의 효과를 시뮬레이션하였다. 자갈 배수는 Fig. 11에서 보이는 것과 같이 2 m 간격으로 10개를 설치하였다.
4. 수치해석 결과
4.1 파괴기준
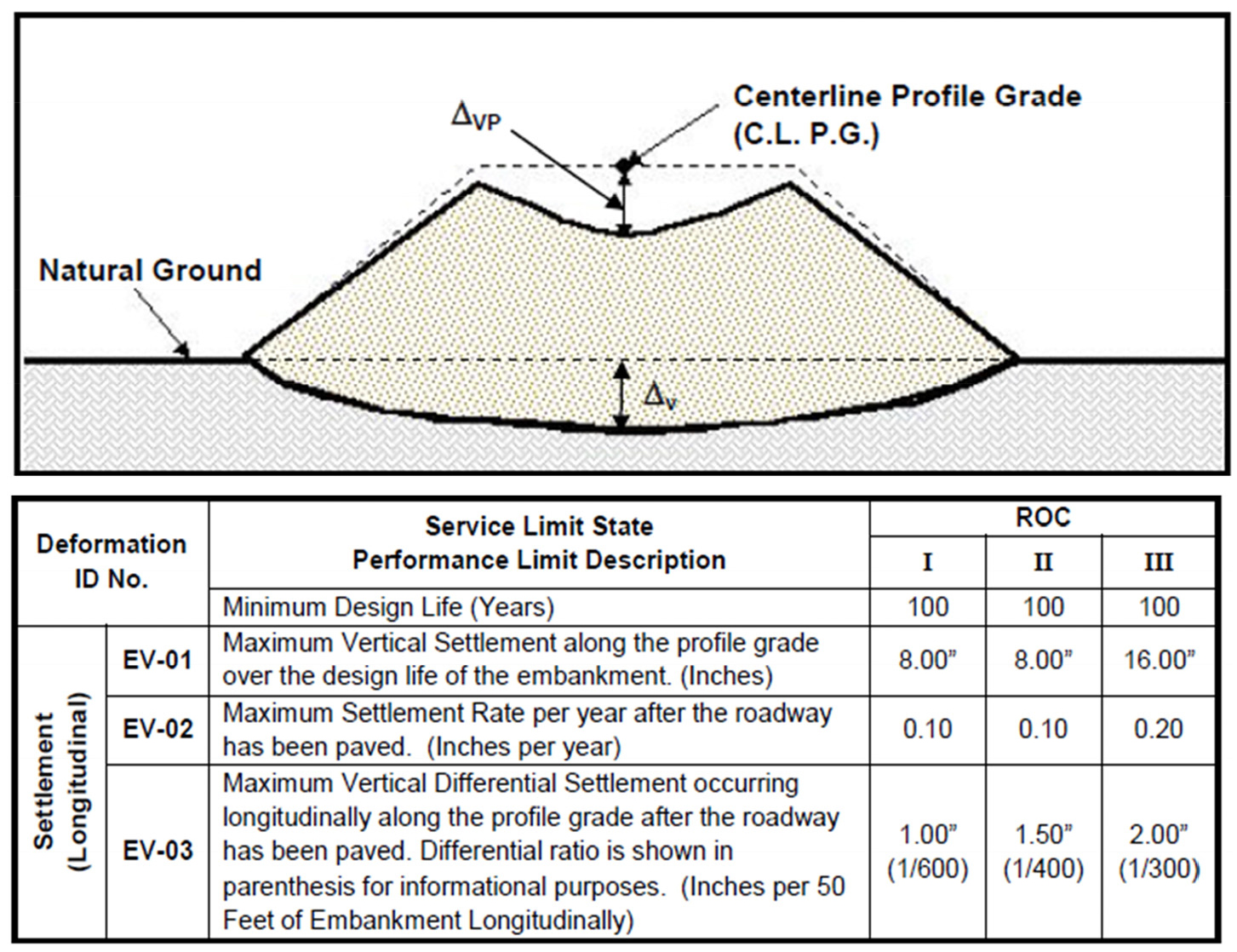
이 연구의 파괴기준을 수립하기 위해, 지반설계매뉴얼(SCDOT, 2008)의 10장에 있는 마루(crest)의 수직 침하에 관한 규정을 채택하였다. 매뉴얼에는 제방 마루의 최대 침하가 16인치 또는 40.64 cm로 제한되어 있는 것이 명시되어 있다(Fig. 12). 이 측정값은 40 cm 이상의 마루변형으로부터 교통흐름 임피던스(impedance in traffic flow)를 규정한 Tokida(2012)의 제안과 일치한다(Fig. 1). Makra(2013)는 액상화가 과잉간극수압이 초기수직유효구속압이나 0.85~1.0의 간극수압비에 도달할 때 발생한다고 하였으며, 이를 바탕으로 과잉간극수압에 의한 파괴기준을 간극수압비가 1.0에 도달했을 때로 정하였다.
4.2 수직 침하 분석 결과
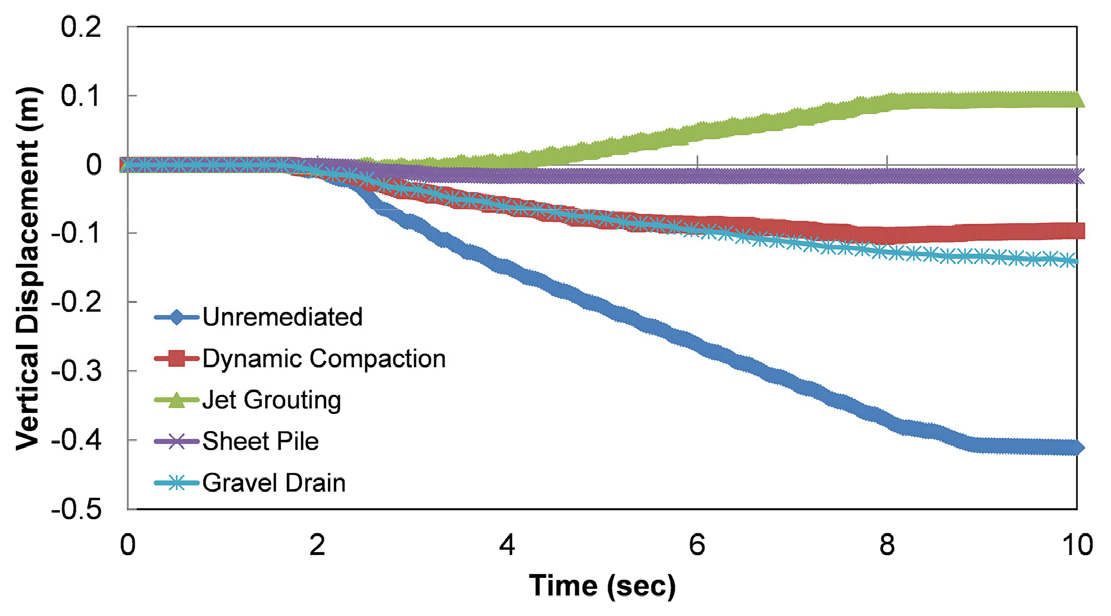
액상화가 발생하면, 제방에 있는 아스팔트 포장도로가 침하되면서 요철 또는 구멍이 생기거나 포장층 라인이 파괴되는 결과를 야기한다. 그렇게 때문에 본 해석 결과에서는 가장 많은 피해가 예상되는 제방의 천단 부분에서의 침하량을 각 공법별로 분석하였다. Fig. 13과 Table 6의 결과를 보면, 시트파일이 수직침하 감소에 가장 효과적이었다. 타이로드를 적용하여 시트파일을 잡아준 것이 수직침하 감소에 영향을 준 것으로 판단되다. 모든 대책방법이 파괴기준을 통과했지만, 제트 그라우팅에서는 침하 대신 히빙 결과가 발생하였다. 그 이유는 기둥의 간극이 막혀서 제트 그라우팅 기둥이 압축될 여지가 없기 때문에 수평으로 퍼져있는 느슨한 모래가 기울어지면서 제방을 위로 밀게 되었기 때문으로 판단된다. 변형운동은 Fig. 14에서 볼 수 있다.
Table 6.
Summary of Values and Performance Remark for Vertical Settlement
| Case | Settlement (cm) | Remarks |
| Unremediated | 41.13 | Failed |
| Dynamic Compaction | 9.72 | Passed |
| Jet Grouting | -9.48 | Passed |
| Sheet Pile Enclosure | 1.66 | Passed |
| Gravel Drain | 14.23 | Passed |
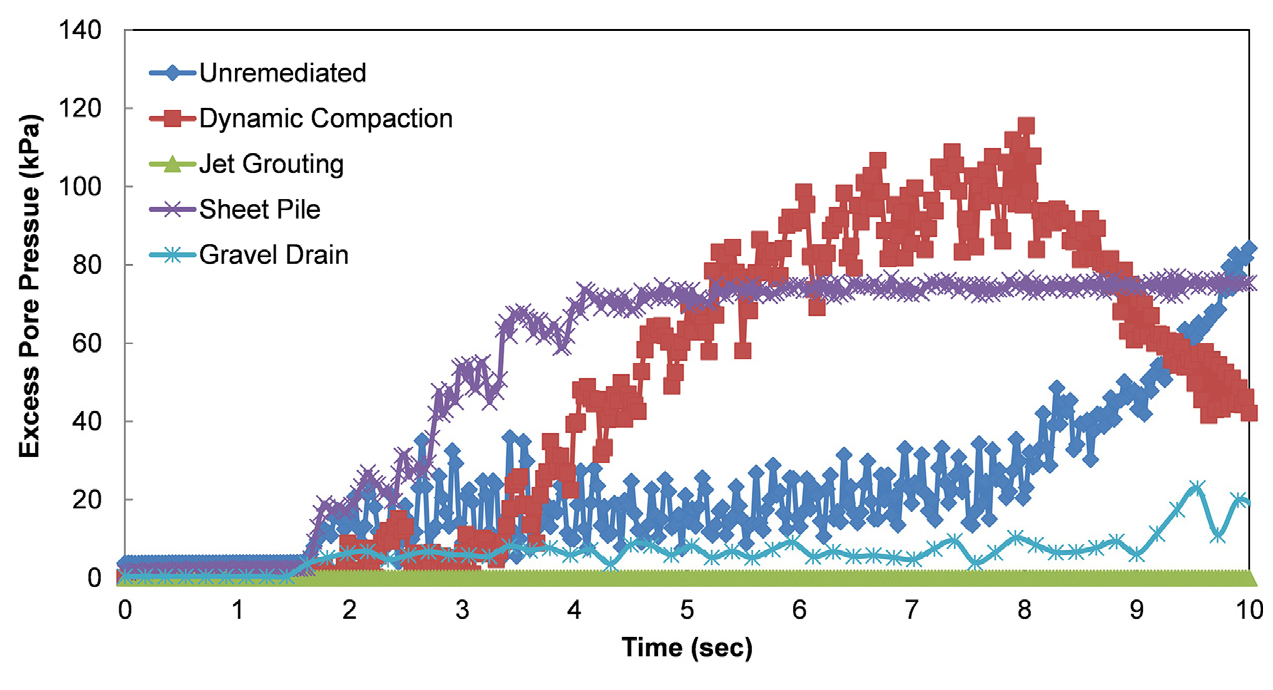
4.3 과잉간극수압비 분석 결과
초기 수직 구속응력은 85 kPa이었다. Fig. 15와 Table 7은 다양한 공법의 과잉간극수압을 보여주며, Table 7에 계산된 최대 과잉간극수압비를 나타내었다. 결과를 보면, 시트파일이 상당한 침하 감소 효과가 있었음에도 불구하고, 과잉간극수압 발생 측면에서 지반을 개선하지 못했다는 것을 알 수 있다. 자갈배수와 제트 그라우팅은 간극유체의 빠른 방출 또는 완전한 간극의 제거로 인해 소산의 가장 좋은 형태를 제공했다. 위의 값은 Fig. 16에서 보이는 층의 특정 지점에서의 결과이다.
Table 7.
Excess Pore Pressure at Upper 1m of LQ Layer
| Case | EPP (kPa) | |
| Unremediated | 84.28 | 0.99 |
| Dynamic Compaction | -42.12 | -0.50 |
| Jet Grouting | 0 | 0 |
| Sheet Pile Enclosure | 75.39 | 0.89 |
| Gravel Drain | 17.56 | 0.21 |
4.4 수치해석 적용방안
액상화 방지대책으로 자주 사용되고 있는 공법 중에서 지반개량, 차수, 배수 등의 방법을 이용한 대표적인 공법들을 적용하여 침하와 간극수압에 대해 분석해보았다. 침하분석에서는 배수가 되는 지반개량, 시트파일, 자갈배수 등은 침하의 거동을 모사하는 데 있어 큰 무리가 없는 것으로 보였다. 그러나 제방 하부에 배수가 되지 않는 제트 그라우팅을 이용한 지반개량의 경우에는 배수가 되지 않으면서 그라우팅이라는 벽에 막혀 침하 대신 히빙이 발생하는 결과가 나타났다. 이러한 결과로 미루어볼 때, 3차원 조건을 2차원 조건으로 모델링할 때에는 배수의 여부에 따라 2차원으로의 모델링 적용 여부를 판단할 필요가 있다. 그러므로 침하 등에 대한 분석을 수행할 때에는 3차원을 2차원으로 모델링하는데 있어 지반구조물의 배수여부를 고려해야 한다.
간극수압 분석결과에서는 시트파일은 주변이 막혀있어서 간극수압을 소산하는 데 어려움이 있음을 잘 보여주었으나, 제트 그라우팅은 전혀 과잉간극수압이 발생하지 않는 결과를 보였다. 제트 그라우팅에서의 비배수 영향이 있는 것으로 보이며, 3차원에서는 다른 결과를 보일 것으로 보인다. 이러한 결과로 미루어볼 때, 그라우팅을 모델링하는 데 있어서 간극수압의 거동을 보기에는 다소 부정확한 점이 있음을 고려해야 한다.
5. 결 론
수치해석을 수행하여 도로제방에서의 다양한 액상화 대책공법의 액상화 저항특성을 분석하여 수치해석 적용방안에 대해 다루었으며, 요약 및 결론은 다음과 같다.
1. 수직침하에 대한 분석결과를 보면, 시트파일 공법을 적용했을 대가 수직침하 감소에 효과적이었는데 시트파일을 잡아주는 타이로드가 시트파일의 측면 변형을 억제하여 지반의 침하감소에 영향을 준 것으로 보인다. 제트 그라우팅에서는 침하 대신 히빙 결과가 발생하는데, 기둥의 간극이 막혀서 제트 그라우팅 기둥이 압축될 여지가 없기 때문에 수평으로 퍼져있는 느슨한 모래가 기울어지면서 제방을 위로 밀게 되었기 때문으로 판단된다.
2. 과잉간극수압의 측면에서는 간극수압의 방출이 잘 되는 자갈배수와 완전히 간극을 제거한 제트 그라우팅이 과잉간극수압의 발생억제와 소산에 효과가 있었다.
3. 수치해석 결과를 종합한 결과, 3차원 조건을 2차원 조건으로 모델링할 때에는 배수의 여부에 따라 2차원으로의 모델링 적용 여부를 판단할 필요가 있으므로 침하 등에 대한 분석을 수행할 때에는 3차원을 2차원으로 모델링하는데 있어 지반구조물의 배수여부를 고려해야 한다. 또한, 간극수압의 거동을 보기에는 완전한 간극발생을 막는 그라우팅을 모델링하는 것이 간극수압 결과를 분석함에 있어 다소 부정확한 점이 있음을 고려해야 한다. 그러므로 이러한 조건에 대한 침하 또는 간극수압 결과를 확인하기 위해서는 2차원 모델링보다는 3차원 모델링을 해야 할 필요가 있다고 판단된다.
4. 본 연구에서는 도로 제방에 대한 액상화 대책공법을 비교하면서 수치해석적 적용방안을 분석하였다. 수치해석을 수행하는 데 있어 공법별로 다양한 조건이 있기 때문에 각 공법의 성능을 단정지을 수 없으며, 다양한 상부 구조물의 특성이 액상화 대책공법에 미치는 영향에 대해서도 분석이 이루어질 필요가 있다. 또한, 본 연구에서는 공법의 종류에 대한 지반내 간극수압과 침하의 변화가 주된 비교대상이었으나, 도로 제방의 조건에 대한 영향 분석은 이루어지지 못했다. 이에 이러한 점들을 보완하여 향후 2차원적 수치해석 한계를 보완한 3차원 수치해석 모델링을 수행하여 도로 제방의 높이, 형상, 도로 재료 특성, 포장 조건 등에 대한 세부적인 연구를 수행할 예정이다. 이러한 연구결과는 향후 실무 엔지니어들이 다양한 액상화 방지 공법의 성능을 평가하고 모델링하는 데 있어 기초자료로 활용하는 데 도움을 줄 것으로 기대한다.